- Set theory
-
This article is about the branch of mathematics. For musical set theory, see Set theory (music).
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics. The language of set theory can be used in the definitions of nearly all mathematical objects.
The modern study of set theory was initiated by Georg Cantor and Richard Dedekind in the 1870s. After the discovery of paradoxes in naive set theory, numerous axiom systems were proposed in the early twentieth century, of which the Zermelo–Fraenkel axioms, with the axiom of choice, are the best-known.
Concepts of set theory are integrated throughout the mathematics curriculum in the United States. Elementary facts about sets and set membership are often taught in primary school, along with Venn diagrams, Euler diagrams, and elementary operations such as set union and intersection. Slightly more advanced concepts such as cardinality are a standard part of the undergraduate mathematics curriculum.
Set theory is commonly employed as a foundational system for mathematics, particularly in the form of Zermelo–Fraenkel set theory with the axiom of choice. Beyond its foundational role, set theory is a branch of mathematics in its own right, with an active research community. Contemporary research into set theory includes a diverse collection of topics, ranging from the structure of the real number line to the study of the consistency of large cardinals.
Contents
History
Mathematical topics typically emerge and evolve through interactions among many researchers. Set theory, however, was founded by a single paper in 1874 by Georg Cantor: "On a Characteristic Property of All Real Algebraic Numbers".[1][2]
Since the 5th century BC, beginning with Greek mathematician Zeno of Elea in the West and early Indian mathematicians in the East, mathematicians had struggled with the concept of infinity. Especially notable is the work of Bernard Bolzano in the first half of the 19th century. The modern understanding of infinity began in 1867-71, with Cantor's work on number theory. An 1872 meeting between Cantor and Richard Dedekind influenced Cantor's thinking and culminated in Cantor's 1874 paper.
Cantor's work initially polarized the mathematicians of his day. While Karl Weierstrass and Dedekind supported Cantor, Leopold Kronecker, now seen as a founder of mathematical constructivism, did not. Cantorian set theory eventually became widespread, due to the utility of Cantorian concepts, such as one-to-one correspondence among sets, his proof that there are more real numbers than integers, and the "infinity of infinities" ("Cantor's paradise") the power set operation gives rise to.
The next wave of excitement in set theory came around 1900, when it was discovered that Cantorian set theory gave rise to several contradictions, called antinomies or paradoxes. Bertrand Russell and Ernst Zermelo independently found the simplest and best known paradox, now called Russell's paradox and involving "the set of all sets that are not members of themselves." This leads to a contradiction, since it must be a member of itself and not a member of itself. In 1899 Cantor had himself posed the question: "what is the cardinal number of the set of all sets?" and obtained a related paradox.
The momentum of set theory was such that debate on the paradoxes did not lead to its abandonment. The work of Zermelo in 1908 and Abraham Fraenkel in 1922 resulted in the canonical axiomatic set theory ZFC, which is thought to be free of paradoxes. The work of analysts such as Henri Lebesgue demonstrated the great mathematical utility of set theory. Axiomatic set theory has become woven into the fabric of modern mathematics.
Basic concepts
Main articles: Set (mathematics) and Algebra of setsSet theory begins with a fundamental binary relation between an object o and a set A. If o is a member (or element) of A, write o ∈ A. Since sets are objects, the membership relation can relate sets as well.
A derived binary relation between two sets is the subset relation, also called set inclusion. If all the members of set A are also members of set B, then A is a subset of B, denoted A ⊆ B. For example, {1,2} is a subset of {1,2,3} , but {1,4} is not. From this definition, it is clear that a set is a subset of itself; in cases where one wishes to avoid this, the term proper subset is defined to exclude this possibility.
Just as arithmetic features binary operations on numbers, set theory features binary operations on sets. The:
- Union of the sets A and B, denoted A ∪ B, is the set of all objects that are a member of A, or B, or both. The union of {1, 2, 3} and {2, 3, 4} is the set {1, 2, 3, 4} .
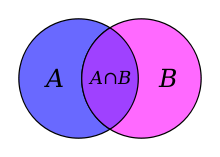
- Intersection of the sets A and B, denoted A ∩ B, is the set of all objects that are members of both A and B. The intersection of {1, 2, 3} and {2, 3, 4} is the set {2, 3} .
- Set difference of U and A, denoted U \ A is the set of all members of U that are not members of A. The set difference {1,2,3} \ {2,3,4} is {1} , while, conversely, the set difference {2,3,4} \ {1,2,3} is {4} . When A is a subset of U, the set difference U \ A is also called the complement of A in U. In this case, if the choice of U is clear from the context, the notation Ac is sometimes used instead of U \ A, particularly if U is a universal set as in the study of Venn diagrams.
- Symmetric difference of sets A and B is the set of all objects that are a member of exactly one of A and B (elements which are in one of the sets, but not in both). For instance, for the sets {1,2,3} and {2,3,4} , the symmetric difference set is {1,4} . It is the set difference of the union and the intersection, (A ∪ B) \ (A ∩ B).
- Cartesian product of A and B, denoted A × B, is the set whose members are all possible ordered pairs (a,b) where a is a member of A and b is a member of B.
- Power set of a set A is the set whose members are all possible subsets of A. For example, the power set of {1, 2} is { {}, {1}, {2}, {1,2} } .
Some basic sets of central importance are the empty set (the unique set containing no elements), the set of natural numbers, and the set of real numbers.
Some ontology
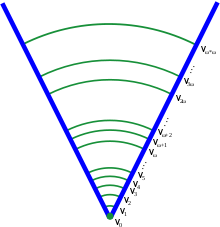
Main article: von Neumann universeA set is pure if all of its members are sets, all members of its members are sets, and so on. For example, the set {{}} containing only the empty set is a nonempty pure set. In modern set theory, it is common to restrict attention to the von Neumann universe of pure sets, and many systems of axiomatic set theory are designed to axiomatize the pure sets only. There are many technical advantages to this restriction, and little generality is lost, since essentially all mathematical concepts can be modeled by pure sets. Sets in the von Neumann universe are organized into a cumulative hierarchy, based on how deeply their members, members of members, etc. are nested. Each set in this hierarchy is assigned (by transfinite recursion) an ordinal number α, known as its rank. The rank of a pure set X is defined to be one more than the least upper bound of the ranks of all members of X. For example, the empty set is assigned rank 0, while the set {{}} containing only the empty set is assigned rank 1. For each ordinal α, the set Vα is defined to consist of all pure sets with rank less than α. The entire von Neumann universe is denoted V.
Axiomatic set theory
Elementary set theory can be studied informally and intuitively, and so can be taught in primary schools using, say, Venn diagrams. The intuitive approach tacitly assumes that a set may be formed from the class of all objects satisfying any particular defining condition. This assumption gives rise to paradoxes, the simplest and best known of which are Russell's paradox and the Burali-Forti paradox. Axiomatic set theory was originally devised to rid set theory of such paradoxes.[3]
The most widely studied systems of axiomatic set theory imply that all sets form a cumulative hierarchy. Such systems come in two flavors, those whose ontology consists of:
- Sets alone. This includes the most common axiomatic set theory, Zermelo–Fraenkel set theory (ZFC), which includes the axiom of choice. Fragments of ZFC include:
- Zermelo set theory, which replaces the axiom schema of replacement with that of separation;
- General set theory, a small fragment of Zermelo set theory sufficient for the Peano axioms and finite sets;
- Kripke-Platek set theory, which omits the axioms of infinity, powerset, and choice, and weakens the axiom schemata of separation and replacement.
- Sets and proper classes. This includes Von Neumann-Bernays-Gödel set theory, which has the same strength as ZFC for theorems about sets alone, and Morse-Kelley set theory, which is stronger than ZFC.
The above systems can be modified to allow urelements, objects that can be members of sets but that are not themselves sets and do not have any members.
The systems of New Foundations NFU (allowing urelements) and NF (lacking them) are not based on a cumulative hierarchy. NF and NFU include a "set of everything," relative to which every set has a complement. In these systems urelements matter, because NF, but not NFU, produces sets for which the axiom of choice does not hold.
Systems of constructive set theory, such as CST, CZF, and IZF, embed their set axioms in intuitionistic logic instead of first order logic. Yet other systems accept standard first order logic but feature a nonstandard membership relation. These include rough set theory and fuzzy set theory, in which the value of an atomic formula embodying the membership relation is not simply True or False. The Boolean-valued models of ZFC are a related subject.
Applications
Many mathematical concepts can be defined precisely using only set theoretic concepts. For example, mathematical structures as diverse as graphs, manifolds, rings, and vector spaces can all be defined as sets satisfying various (axiomatic) properties. Equivalence and order relations are ubiquitous in mathematics, and the theory of mathematical relations can be described in set theory.
Set theory is also a promising foundational system for much of mathematics. Since the publication of the first volume of Principia Mathematica, it has been claimed that most or even all mathematical theorems can be derived using an aptly designed set of axioms for set theory, augmented with many definitions, using first or second order logic. For example, properties of the natural and real numbers can be derived within set theory, as each number system can be identified with a set of equivalence classes under a suitable equivalence relation whose field is some infinite set.
Set theory as a foundation for mathematical analysis, topology, abstract algebra, and discrete mathematics is likewise uncontroversial; mathematicians accept that (in principle) theorems in these areas can be derived from the relevant definitions and the axioms of set theory. Few full derivations of complex mathematical theorems from set theory have been formally verified, however, because such formal derivations are often much longer than the natural language proofs mathematicians commonly present. One verification project, Metamath, includes derivations of more than 10,000 theorems starting from the ZFC axioms and using first order logic.
Areas of study
Set theory is a major area of research in mathematics, with many interrelated subfields.
Combinatorial set theory
Main article: Infinitary combinatoricsCombinatorial set theory concerns extensions of finite combinatorics to infinite sets. This includes the study of cardinal arithmetic and the study of extensions of Ramsey's theorem such as the Erdős–Rado theorem.
Descriptive set theory
Main article: Descriptive set theoryDescriptive set theory is the study of subsets of the real line and, more generally, subsets of Polish spaces. It begins with the study of pointclasses in the Borel hierarchy and extends to the study of more complex hierarchies such as the projective hierarchy and the Wadge hierarchy. Many properties of Borel sets can be established in ZFC, but proving these properties hold for more complicated sets requires additional axioms related to determinacy and large cardinals.
The field of effective descriptive set theory is between set theory and recursion theory. It includes the study of lightface pointclasses, and is closely related to hyperarithmetical theory. In many cases, results of classical descriptive set theory have effective versions; in some cases, new results are obtained by proving the effective version first and then extending ("relativizing") it to make it more broadly applicable.
A recent area of research concerns Borel equivalence relations and more complicated definable equivalence relations. This has important applications to the study of invariants in many fields of mathematics.
Fuzzy set theory
Main article: Fuzzy set theoryIn set theory as Cantor defined and Zermelo and Fraenkel axiomatized, an object is either a member of a set or not. In fuzzy set theory this condition was relaxed by Lotfi A. Zadeh so an object has a degree of membership in a set, as number between 0 and 1. For example, the degree of membership of a person in the set of "tall people" is more flexible than a simple yes or no answer and can be a real number such as 0.75.
Inner model theory
Main article: Inner model theoryAn inner model of Zermelo–Fraenkel set theory (ZF) is a transitive class that includes all the ordinals and satisfies all the axioms of ZF. The canonical example is the constructible universe L developed by Gödel. One reason that the study of inner models is of interest is that it can be used to prove consistency results. For example, it can be shown that regardless whether a model V of ZF satisfies the continuum hypothesis or the axiom of choice, the inner model L constructed inside the original model will satisfy both the generalized continuum hypothesis and the axiom of choice. Thus the assumption that ZF is consistent (has any model whatsoever) implies that ZF together with these two principles is consistent.
The study of inner models is common in the study of determinacy and large cardinals, especially when considering axioms such as the axiom of determinacy that contradict the axiom of choice. Even if a fixed model of set theory satisfies the axiom of choice, it is possible for an inner model to fail to satisfy the axiom of choice. For example, the existence of sufficiently large cardinals implies that there is an inner model satisfying the axiom of determinacy (and thus not satisfying the axiom of choice).[4]
Large cardinals
Main article: Large cardinal propertyA large cardinal is a cardinal number with an extra property. Many such properties are studied, including inaccessible cardinals, measurable cardinals, and many more. These properties typically imply the cardinal number must be very large, with the existence of a cardinal with the specified property unprovable in Zermelo-Fraenkel set theory.
Determinacy
Main article: DeterminacyDeterminacy refers to the fact that, under appropriate assumptions, certain two-player games of perfect information are determined from the start in the sense that one player must have a winning strategy. The existence of these strategies has important consequences in descriptive set theory, as the assumption that a broader class of games is determined often implies that a broader class of sets will have a topological property. The axiom of determinacy (AD) is an important object of study; although incompatible with the axiom of choice, AD implies that all subsets of the real line are well behaved (in particular, measurable and with the perfect set property). AD can be used to prove that the Wadge degrees have an elegant structure.
Forcing
Main article: Forcing (mathematics)Paul Cohen invented the method of forcing while searching for a model of ZFC in which the axiom of choice or the continuum hypothesis fails. Forcing adjoins to some given model of set theory additional sets in order to create a larger model with properties determined (i.e. "forced") by the construction and the original model. For example, Cohen's construction adjoins additional subsets of the natural numbers without changing any of the cardinal numbers of the original model. Forcing is also one of two methods for proving relative consistency by finitistic methods, the other method being Boolean-valued models.
Cardinal invariants
Main article: Cardinal invariantA cardinal invariant is a property of the real line measured by a cardinal number. For example, a well-studied invariant is the smallest cardinality of a collection of meagre sets of reals whose union is the entire real line. These are invariants in the sense that any two isomorphic models of set theory must give the same cardinal for each invariant. Many cardinal invariants have been studied, and the relationships between them are often complex and related to axioms of set theory.
Set-theoretic topology
Main article: Set-theoretic topologySet-theoretic topology studies questions of general topology that are set-theoretic in nature or that require advanced methods of set theory for their solution. Many of these theorems are independent of ZFC, requiring stronger axioms for their proof. A famous problem is the normal Moore space question, a question in general topology that was the subject of intense research. The answer to the normal Moore space question was eventually proved to be independent of ZFC.
Objections to set theory as a foundation for mathematics
From set theory's inception, some mathematicians objected to it as a foundation for mathematics, arguing, for example, that it is just a game which includes elements of fantasy.[citation needed] The most common objection to set theory, one Kronecker voiced in set theory's earliest years, starts from the constructivist view that mathematics is loosely related to computation. If this view is granted, then the treatment of infinite sets, both in naive and in axiomatic set theory, introduces into mathematics methods and objects that are not computable even in principle. Ludwig Wittgenstein questioned the way Zermelo–Fraenkel set theory handled infinities. Wittgenstein's views about the foundations of mathematics were later criticised by Georg Kreisel and Paul Bernays, and closely investigated by Crispin Wright, among others.
Category theorists have proposed topos theory as an alternative to traditional axiomatic set theory. Topos theory can interpret various alternatives to that theory, such as constructivism, finite set theory, and computable set theory.[citation needed]
See also
- Category theory
- List of set theory topics
- Musical set theory concerns the application of combinatorics and group theory to music; beyond the fact that it uses finite sets it has nothing to do with mathematical set theory of any kind. In the last two decades, transformational theory in music has taken the concepts of mathematical set theory more rigorously (see Lewin 1987).
- Relational model - Borrows from Set Theory.
Notes
- ^ G. Cantor, Über eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen, Crelles Journal f. Mathematik 77 (1874) 258 - 262.
- ^ Philip Johnson, 1972, A History of Set Theory, Prindle, Weber & Schmidt ISBN 0871501546
- ^ In his 1925, John von Neumann observed that "set theory in its first, "naive" version, due to Cantor, led to contradictions. These are the well-known antinomies of the set of all sets that do not contain themselves (Russell), of the set of all transfinte ordinal numbers (Burali-Forti), and the set of all finitely definable real numbers (Richard)." He goes on to observe that two "tendencies" were attempting to "rehabilitate" set theory. Of the first effort, exemplified by Bertrand Russell, Julius König, Hermann Weyl and L. E. J. Brouwer, von Neumann called the "overall effect of their activity . . . devastating". With regards to the axiomatic method employed by second group composed of Zermelo, Abraham Fraenkel and Arthur Moritz Schoenflies, von Neumann worried that "We see only that the known modes of inference leading to the antinomies fail, but who knows where there are not others?" and he set to the task, "in the spirit of the second group", to "produce, by means of a finite number of purely formal operations . . . all the sets that we want to see formed" but not allow for the antinomies. (All quotes from von Neumann 1925 reprinted in van Heijenoort, Jean (1967, third printing 1976), "From Frege to Gödel: A Source Book in Mathematical Logic, 1979-1931", Harvard University Press, Cambridge MA, ISBN 0-674-32449-8 (pbk). A synopsis of the history, written by van Heijenoort, can be found in the comments that precede von Neumann's 1925.
- ^ Jech, Thomas (2003), Set Theory: Third Millennium Edition, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-44085-7, p. 642.
Further reading
- Devlin, Keith, (2nd ed.) 1993. The Joy of Sets. Springer Verlag, ISBN 0-387-94094-4
- Ferreirós, Jose, 2007 (1999). Labyrinth of Thought: A history of set theory and its role in modern mathematics. Basel, Birkhäuser. ISBN 978-3-7643-8349-7
- Johnson, Philip, 1972. A History of Set Theory. Prindle, Weber & Schmidt ISBN 0871501546
- Kunen, Kenneth, 1980. Set Theory: An Introduction to Independence Proofs. North-Holland, ISBN 0-444-85401-0.
- Tiles, Mary, 2004 (1989). The Philosophy of Set Theory: An Historical Introduction to Cantor's Paradise. Dover Publications.
External links
- Foreman, M., Akihiro Kanamori, eds. Handbook of Set Theory. 3 vols., 2010. Each chapter surveys some aspect of contemporary research in set theory. Does not cover established elementary set theory, on which see Devlin (1993).
Areas of mathematics Areas Arithmetic · Algebra (elementary – linear – multilinear – abstract) · Geometry (Discrete geometry – Algebraic geometry – Differential geometry) · Calculus/Analysis · Set theory · Logic · Category theory · Number theory · Combinatorics · Graph theory · Topology · Lie theory · Differential equations/Dynamical systems · Mathematical physics · Numerical analysis · Computation · Information theory · Probability · Statistics · Optimization · Control theory · Game theory
Divisions Categories:
Wikimedia Foundation. 2010.