- Thermodynamic system
-
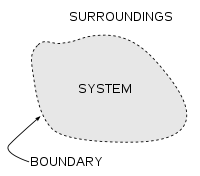
A thermodynamic system is a precisely defined macroscopic region of the universe, often called a physical system, that is studied using the principles of thermodynamics.
All space in the universe outside the thermodynamic system is known as the surroundings, the environment, or a reservoir. A system is separated from its surroundings by a boundary which may be notional or real, but which by convention delimits a finite volume. Exchanges of work, heat, or matter between the system and the surroundings may take place across this boundary. Thermodynamic systems are often classified by specifying the nature of the exchanges that are allowed to occur across its boundary.
A thermodynamic system is characterized and defined by a set of thermodynamic parameters associated with the system. The parameters are experimentally measurable macroscopic properties, such as volume, pressure, temperature, electric field, and others.
The set of thermodynamic parameters necessary to uniquely define a system is called the thermodynamic state of a system. The state of a system is expressed as a functional relationship, the equation of state, between its parameters. A system is in thermodynamic equilibrium when the state of the system does not change with time.
Originally, in 1824, Sadi Carnot described a thermodynamic system as the working substance under study.
Contents
Overview
Thermodynamics describes the physics of matter using the concept of the thermodynamic system, a region of the universe that is under study. All quantities, such as pressure or mechanical work, in an equation refer to the system unless labeled otherwise. As thermodynamics is fundamentally concerned with the flow and balance of energy and matter, systems are distinguished depending on the kinds of interaction they undergo and the types of energy they exchange with the surrounding environment.
Interactions of thermodynamic systems Type of system Mass flow Work Heat Open 


Closed 


Isolated 


Isolated systems are completely isolated from their environment. They do not exchange heat, work or matter with their environment. An example of an isolated system is a completely insulated rigid container, such as a completely insulated gas cylinder. Closed systems are able to exchange energy (heat and work) but not matter with their environment. A greenhouse is an example of a closed system exchanging heat but not work with its environment. Whether a system exchanges heat, work or both is usually thought of as a property of its boundary. Open systems may exchange any form of energy as well as matter with their environment. A boundary allowing matter exchange is called permeable. The ocean would be an example of an open system.
In practice, a system can never be absolutely isolated from its environment, because there is always at least some slight coupling, such as gravitational attraction. In analyzing a system in steady-state, the energy into the system is equal to the energy leaving the system [1].
An example system is the system of hot liquid water and solid table salt in a sealed, insulated test tube held in a vacuum (the surroundings). The test tube constantly loses heat in the form of black-body radiation, but the heat loss progresses very slowly. If there is another process going on in the test tube, for example the dissolution of the salt crystals, it will probably occur so quickly that any heat lost to the test tube during that time can be neglected. Thermodynamics in general does not measure time, but it does sometimes accept limitations on the time frame of a process.
History
The first to develop the concept of a thermodynamic system was the French physicist Sadi Carnot whose 1824 Reflections on the Motive Power of Fire studied what he called the working substance, e.g., typically a body of water vapor, in steam engines, in regards to the system's ability to do work when heat is applied to it. The working substance could be put in contact with either a heat reservoir (a boiler), a cold reservoir (a stream of cold water), or a piston (to which the working body could do work by pushing on it). In 1850, the German physicist Rudolf Clausius generalized this picture to include the concept of the surroundings, and began referring to the system as a "working body." In his 1850 manuscript On the Motive Power of Fire, Clausius wrote:
“ "With every change of volume (to the working body) a certain amount work must be done by the gas or upon it, since by its expansion it overcomes an external pressure, and since its compression can be brought about only by an exertion of external pressure. To this excess of work done by the gas or upon it there must correspond, by our principle, a proportional excess of heat consumed or produced, and the gas cannot give up to the "surrounding medium" the same amount of heat as it receives." ” The article Carnot heat engine shows the original piston-and-cylinder diagram used by Carnot in discussing his ideal engine; below, we see the Carnot engine as is typically modeled in current use:
 Carnot engine diagram (modern) - where heat flows from a high temperature TH furnace through the fluid of the "working body" (working substance) and into the cold sink TC, thus forcing the working substance to do mechanical work W on the surroundings, via cycles of contractions and expansions.
Carnot engine diagram (modern) - where heat flows from a high temperature TH furnace through the fluid of the "working body" (working substance) and into the cold sink TC, thus forcing the working substance to do mechanical work W on the surroundings, via cycles of contractions and expansions.
In the diagram shown, the "working body" (system), a term introduced by Clausius in 1850, can be any fluid or vapor body through which heat Q can be introduced or transmitted through to produce work. In 1824, Sadi Carnot, in his famous paper Reflections on the Motive Power of Fire, had postulated that the fluid body could be any substance capable of expansion, such as vapor of water, vapor of alcohol, vapor of mercury, a permanent gas, or air, etc. Although, in these early years, engines came in a number of configurations, typically QH was supplied by a boiler, wherein water was boiled over a furnace; QC was typically a stream of cold flowing water in the form of a condenser located on a separate part of the engine. The output work W here is the movement of the piston as it is used to turn a crank-arm, which was then typically used to turn a pulley so to lift water out of flooded salt mines. Carnot defined work as "weight lifted through a height."
Boundary
A system boundary is a real or imaginary two-dimensional closed surface that encloses or demarcates the volume or region that a thermodynamic system occupies, across which quantities such as heat, mass, or work can flow.[1] In short, a thermodynamic boundary is a geometrical division between a system and its surroundings. Topologically, it is usually considered to be nearly or piecewise smoothly homeomorphic with a two-sphere, because a system is usually considered to be simply connected.
Boundaries can also be fixed (e.g. a constant volume reactor) or moveable (e.g. a piston). For example, in an engine, a fixed boundary means the piston is locked at its position; as such, a constant volume process occurs. In that same engine, a moveable boundary allows the piston to move in and out. Boundaries may be real or imaginary. For closed systems, boundaries are real while for open system boundaries are often imaginary. For theoretical purposes, a boundary may be declared to be adiabatic, isothermal, diathermal, insulating, permeable, or semipermeable, but actual physical materials that provide such idealized properties are not always readily available.
Anything that passes across the boundary that effects a change in the internal energy needs to be accounted for in the energy balance equation. The volume can be the region surrounding a single atom resonating energy, such as Max Planck defined in 1900; it can be a body of steam or air in a steam engine, such as Sadi Carnot defined in 1824; it can be the body of a tropical cyclone, such as Kerry Emanuel theorized in 1986 in the field of atmospheric thermodynamics; it could also be just one nuclide (i.e. a system of quarks) as hypothesized in quantum thermodynamics.
Surroundings
See also: Environment (systems)The system is the part of the universe being studied, while the surroundings is the remainder of the universe that lies outside the boundaries of the system. It is also known as the environment, and the reservoir. Depending on the type of system, it may interact with the system by exchanging mass, energy (including heat and work), momentum, electric charge, or other conserved properties. The environment is ignored in analysis of the system, except in regards to these interactions.
Open system
 During steady, continuous operation, an energy balance applied to an open system equates shaft work performed by the system to heat added plus net enthalpy added.
During steady, continuous operation, an energy balance applied to an open system equates shaft work performed by the system to heat added plus net enthalpy added.
In open systems, matter may flow in and out of the system boundaries. The first law of thermodynamics for open systems states: the increase in the internal energy of a system is equal to the amount of energy added to the system by matter flowing in and by heating, minus the amount lost by matter flowing out and in the form of work done by the system. The first law for open systems is given by:
where Uin is the average internal energy entering the system and Uout is the average internal energy leaving the system
The region of space enclosed by open system boundaries is usually called a control volume, and it may or may not correspond to physical walls. If we choose the shape of the control volume such that all flow in or out occurs perpendicular to its surface, then the flow of matter into the system performs work as if it were a piston of fluid pushing mass into the system, and the system performs work on the flow of matter out as if it were driving a piston of fluid. There are then two types of work performed: flow work described above which is performed on the fluid (this is also often called PV work) and shaft work which may be performed on some mechanical device. These two types of work are expressed in the equation:
Substitution into the equation above for the control volume cv yields:
The definition of enthalpy, H, permits us to use this thermodynamic potential to account for both internal energy and PV work in fluids for open systems:
During steady-state operation of a device (see turbine, pump, and engine), any system property within the control volume is independent of time. Therefore, the internal energy of the system enclosed by the control volume remains constant, which implies that dUcv in the expression above may be set equal to zero. This yields a useful expression for the power generation or requirement for these devices in the absence of chemical reactions:
This expression is described by the diagram above.
Closed system
In a closed system, no mass may be transferred in or out of the system boundaries. The system will always contain the same amount of matter, but heat and work can be exchanged across the boundary of the system. Whether a system can exchange heat, work, or both is dependent on the property of its boundary.
- Adiabatic boundary – not allowing any heat exchange
- Rigid boundary – not allowing exchange of work
One example is fluid being compressed by a piston in a cylinder. Another example of a closed system is a bomb calorimeter, a type of constant-volume calorimeter used in measuring the heat of combustion of a particular reaction. Electrical energy travels across the boundary to produce a spark between the electrodes and initiates combustion. Heat transfer occurs across the boundary after combustion but no mass transfer takes place either way.
Beginning with the first law of thermodynamics for an open system, this is expressed as:
where U is internal energy, Q is heat transfer, W is work, and since no mass is transferred in or out of the system, both expressions involving mass flow, , zeroes, and the first law of thermodynamics for a closed system is derived. The first law of thermodynamics for a closed system states that the amount of internal energy within the system equals the difference between the amount of heat added to or extracted from the system and the work done by or to the system. The first law for closed systems is stated by:
- dU = δQ − δW
where U is the average internal energy within the system, Q is the heat added to or extracted from the system and W is the work done by or to the system.
Substituting the amount of work needed to accomplish a reversible process, which is stated by:
- δW = PdV
where P is the measured pressure and V is the volume, and the heat required to accomplish a reversible process stated by the second law of thermodynamics, the universal principle of entropy, stated by:
- δQ = TdS
where T is the absolute temperature and S is the entropy of the system, derives the fundamental thermodynamic relationship used to compute changes in internal energy, which is expressed as:
- δU = TdS − PdV
For a simple system, with only one type of particle (atom or molecule), a closed system amounts to a constant number of particles. However, for systems which are undergoing a chemical reaction, there may be all sorts of molecules being generated and destroyed by the reaction process. In this case, the fact that the system is closed is expressed by stating that the total number of each elemental atom is conserved, no matter what kind of molecule it may be a part of. Mathematically:

where Nj is the number of j-type molecules, aij is the number of atoms of element i in molecule j and bi0 is the total number of atoms of element i in the system, which remains constant, since the system is closed. There will be one such equation for each different element in the system.
Isolated system
An isolated system is more restrictive than a closed system as it does not interact with its surroundings in any way. Mass and energy remains constant within the system, and no energy or mass transfer takes place across the boundary. As time passes in an isolated system, internal differences in the system tend to even out and pressures and temperatures tend to equalize, as do density differences. A system in which all equalizing processes have gone practically to completion is considered to be in a state of thermodynamic equilibrium.
Truly isolated physical systems do not exist in reality (except perhaps for the universe as a whole), because, for example, there is always gravity between a system with mass and masses elsewhere. However, real systems may behave nearly as an isolated system for finite (possibly very long) times. The concept of an isolated system can serve as a useful model approximating many real-world situations. It is an acceptable idealization used in constructing mathematical models of certain natural phenomena.
In the attempt to justify the postulate of entropy increase in the second law of thermodynamics, Boltzmann’s H-theorem used equations which assumed a system (for example, a gas) was isolated. That is all the mechanical degrees of freedom could be specified, treating the walls simply as mirror boundary conditions. This inevitably led to Loschmidt's paradox. However, if the stochastic behavior of the molecules in actual walls is considered, along with the randomizing effect of the ambient, background thermal radiation, Boltzmann’s assumption of molecular chaos can be justified.
The second law of thermodynamics is only true for isolated systems. It states that the entropy of an isolated system not in equilibrium will tend to increase over time, approaching maximum value at equilibrium. Overall, in an isolated system, the available energy can never increase, and it complement, entropy, can never decrease. A closed system's entropy can decrease.
It is important to note that isolated systems are not equivalent to closed systems. Closed systems cannot exchange matter with the surroundings, but can exchange energy. Isolated systems can exchange neither matter nor energy with their surroundings, and as such are only theoretical and do not exist in reality (except, possibly, the entire universe).
It is worth noting that 'closed system' is often used in thermodynamics discussions when 'isolated system' would be correct - i.e. there is an assumption that energy does not enter or leave the system.
Systems in equilibrium
At thermodynamic equilibrium, a system's properties are, by definition, unchanging in time. Systems in equilibrium are much simpler and easier to understand than systems which are not in equilibrium. Often, when analyzing a thermodynamic process, it can be assumed that each intermediate state in the process is at equilibrium. This will also considerably simplify the analysis.
In isolated systems it is consistently observed that as time goes on internal rearrangements diminish and stable conditions are approached. Pressures and temperatures tend to equalize, and matter arranges itself into one or a few relatively homogeneous phases. A system in which all processes of change have gone practically to completion is considered to be in a state of thermodynamic equilibrium. The thermodynamic properties of a system in equilibrium are unchanging in time. Equilibrium system states are much easier to describe in a deterministic manner than non-equilibrium states.
In thermodynamic processes, large departures from equilibrium during intermediate steps are associated with increases in entropy and increases in the production of heat rather than useful work. It can be shown that for a process to be reversible, each step in the process must be reversible. For a step in a process to be reversible, the system must be in equilibrium throughout the step. That ideal cannot be accomplished in practice because no step can be taken without perturbing the system from equilibrium, but the ideal can be approached by making changes slowly.
See also
References
- ^ Perrot, Pierre (1998). A to Z of Thermodynamics. Oxford University Press. ISBN 0-19-856552-6.
- Abbott, M.M. and H.G. van Hess. Thermodynamics with Chemical Applications. 2nd ed. McGraw Hill, 1989.
- Halliday, David, Robert Resnick, and Jearl Walker. Fundamentals of Physics. 8th ed. Wiley, 2008.
- Moran, Michael J. and Howard N. Shapiro. Fundamentals of Engineering Thermodynamics. 6th ed. Wiley, 2008.
External links
Categories:- Thermodynamics
- Dynamical systems
- Physical systems
Wikimedia Foundation. 2010.