- Hexany
-
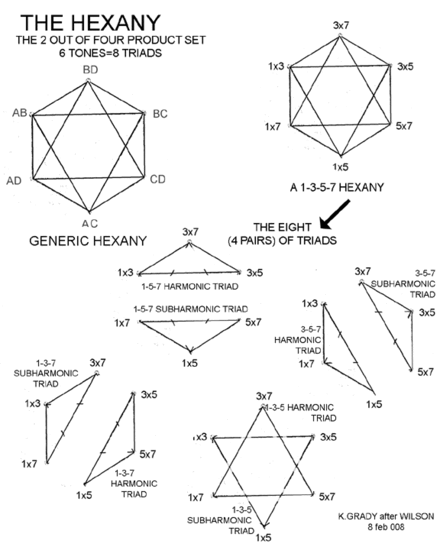
In music theory, the hexany is a six-note just intonation scale, with the notes placed on the vertices of an octahedron, equivalently the faces of a cube. The notes are arranged so that every edge of the octahedron joins together notes that make a consonant dyad, and every face joins together the notes of a consonant triad.
This makes a "musical geometry" with the geometrical form of the octahedron. It has eight just intonation triads in a scale of only six notes, and each triad has two notes in common with three of the other chords, arranged in a musically symmetrical fashion due to the symmetry of the octahedron it is based on.
The Hexany is the invention of Erv Wilson[1] and represents one of the simplest structures found in his Combination Product Sets, which are obtained as successive cross sections of an n-dimensional cube. The numbers of vertices follow the numbers in Pascal's triangle. The hexany is the third cross section of the four-dimensional cube. "Hexany is the name that Erv Wilson gave to the six notes in the 2-out-of-4 combination product set (abbreviated as 2\4 CPOS)."[2]
Contents
Tuning
The four dimensions of the hypercube are usually tuned to distinct primes (sometimes to odd numbers) and a single step in each dimension corresponds to multiplying the frequency by that prime. The notes are then usually reduced to the octave (by repeated division by 2) using octave equivalence.
For example, for a 2 3 5 7 hexany, assign 2 3 5 7, to the four dimensions. Then to obtain the octahedron as a diagonal cross section of the hypercube, use all permutations of (1,1,0,0) as the coords. There for instance, (0,0,1,1) moves one step in the "5" dimension and one step in the "7" dimension and so would be tuned as 5×7.
So, to make the complete hexany, multiply the primes together in pairs to give six numbers: 2×3, 2×5, 2×7, 3×5, 3×7, and 5×7 (or 2×3×1×1, 2×1×5×1, 2×1×1×7, 1×3×5×1, 1×3×1×7 and 1×1×5×7). This shows the context in 4D.

In this picture of a hypercube, the six hexany vertices are shown in yellow, and four of the vertices are shown connected (in green). The other two vertices join to them to make the octahedron. All the sides of the octahedron are diagonals of squares, so are the same length (root two), so it is a regular octahedron — the "squashed" appearance is because it is rotated into the fourth dimension.
You can see the tetrahedral slices of the hypercube similarly - the red vertices can be joined together to make a regular tetrahedron, and the purple vertices likewise. So going from one of the blue points to the other you have 1 vertex, 4 for the red tetrahedron, 6 vertices for the yellow octahedron (hexany), 4 for the purple tetrahedron and 1 more vertex to make up the complete cube.
If one finds it a bit baffling that's to be expected — a few people, like Alicia Stott, have been able to think four-dimensionally but it is beyond most of us.
Then for example the face with vertices 3×5, 2×5, 5×7 is an otonal (major type) chord since it can be written as 5×(2, 3, 7), using low numbered harmonics. The 5×7, 3×7, 3×5 is a utonal (minor type) chord since it can be written as 3×5×7×(1/3, 1/5, 1/7), using low-numbered subharmonics.
Musical lattices are often constructed with the octave dimension omitted. Then the hexanies show up in the 3D lattices as octahedra between the alternating otonal and utonal tetrahedra (for tetrads). However the octave (2) dimension is shown in the diagram above to bring out its 4D context, and help make the connection with the Pascal's triangle construction via the hypercube.
To make this into a conventional scale with 1/1 as the first note, first reduce all the notes to the octave. Since the scale doesn't have a 1/1 yet, choose one of the notes, it doesn't matter which. Let's choose 5×7. Divide all the notes by 5×7 to get: 1/1 8/7 6/5 48/35 8/5 12/7 2/1 (up to octave reduction). The ratios notation here shows the ratio of the frequencies of the notes. So for instance if the 1/1 is 500 hertz, then 6/5 is 600 hertz, and so forth.
This figure shows the hexany in its more usual 3D representation:
Relationship to Pascal's triangle
The complete row of Pascal's triangle for the hypercube in this construction runs 1 (single vertex), 4 (tetrahedron tetrad), 6 (hexany), 4 (another tetrad), 1. The idea generalises to other numbers of dimensions – for instance, the cross-sections of a five-dimensional cube give two versions of the dekany – a ten-note scale rich in tetrads, triads and dyads, which also contains many hexanies.
In six dimensions the same construction gives the twenty-note eikosany which is even richer in chords. It has pentads, tetrads, and triads as well as hexanies and dekanies.
In the case of the three-dimensional cube, it is usual to consider the entire cube as a single eight-note scale, the octany – the cross-sections then are 1, 3 (triad), 3 (another triad), 1, taken along any of the four main diagonals of the cube.
Coordinates for the Pascal's triangle of combination product sets
First row (square):
00
10 01
11Second row (cube or octony):
000
100 010 001 triad (triangle)
110 101 011 triad (triangle)
111Third row (hypercube)
0000
1000 0100 0010 0001 tetrad (tetrahedron or 3-simplex)
1100 1010 1001 0110 0101 0011 hexany (octahedron)
1110 1101 1011 0111 tetrad
1111The octahedron there is the edge dual of the tetrahedron, or rectified tetrahedron
Fourth row (5-dimensional cube)
00000
10000 01000 00100 00010 00001 pentad (4-simplex or pentachoron - four dimensional tetrahedron)
11000 10100 10010 10001 01100 01010 01001 00110 00101 00011 2)5 dekany (10 vertices, rectified 4-simplex)
00111 01011 01101 01110 10011 10101 10110 11001 11010 11100 3)5 dekany (10 vertices)
01111 10111 11011 11101 11110 pentad
11111The rectified 4-simplex for the dekany is also known as the dispentachoron
Fifth row (6-dimensional cube
000000
100000 010000 001000 000100 000010 000001 hexad (5-simplex or hexateron - five dimensional tetrahedron)
110000 101000 100100 100010 100001 011000 010100 010010 010001 001100 001010 001001 000110 000101 000011 2)6 pentadekany (15 vertices, rectified 5-simplex)
111000 110100 110010 110001 101100 101010 101001 100110 100101 100011 011100 011010 011001 010110 010101 010011 001110 001101 001011 000111 eikosany (20 vertices birectified 5-simplex)
001111 010111 011011 011101 011110 100111 101011 101101 101110 110011 110101 110110 111001 111010 111100 4)6 pentadekany (15 vertices)
011111 101111 110111 111011 111101 111110 hexad
111111It is easy to see that the geometric figure for the dekany is the edge dual of the 4-simplex and the one for the pentadekany is the edge dual of the 5-simplex.
To see this, in the figure of the octahedron in the hypercube, scale the entire figure by 1/2 about the origin (blue vertex). The octahedron vertices will move to the midpoints of the original tetrahedron edges (joining the red vertices in the figure).
So - similarly the dekany vertices when scaled by 1/2 move to the midpoints of the 4-simplex edges, and the pentadekany vertices move to the midpoints of the 5-simplex edges, and so on in all the higher dimensions.
The eikosany vertices when scaled by 1/3 move to the centres of the 2D faces of the 5-simplex. To see that, note that in a 3D cube, 111 when scaled by 1/3 moves to the midpoint of 100 010 001 (each edge vector subtends the same distance along the long diagonal of the cube). So 11100 moves to the centre of the equilateral triangle with coords 10000 01000 00100 and similarly for all the other eikosany vertices.
So - the geometric figure for the eikosany is the 2D face dual of the 5-simplex or birectified 5-simplex. Similarly for the 3)7, 3)8 etc figures in all higher dimensions.
Similarly in eight dimensions, the figure you get using all permutations of 4 out of 8 is the 3D face dual of the 7-simplex, or 3-rectified 7-simplex (since 1111 scaled by 1/4 moves to the centre of the 3D regular tetrahedron face 1000 0100 0010 0001), and so on.
Composers
Composers including Kraig Grady, Daniel James Wolf, and Joseph Pehrson have used pitch structures based on hexanies.
See also
References
- ^ Chalmers, John H. (1993). Divisions of the Tetrachord: a Prolegomenon to the Construction of Musical Scales, p.116. Frog Peak Music. ISBN 9780945996040.
- ^ [author missing] (1993). Musicworks, Issues 55-60, p.43. Music Gallery.
Further reading
- Grady, Kraig (1991), "Ervin Wilson's Hexany", Just Intonation 7 (1): 8–11
- Schiemer, Greg, "Tempered Dekanies: Chorus effect using microtonal intervals based on just intonation" ([dead link]), Proceedings of the 7th International Conference on Music Perception and Cognition, Sydney, 2002: 300–302, http://www.uow.info/crearts/staff/schiemer/ICMPC7.pdf (see the Background section)
External links
- "Some Hexany and Hexany Diamond Lattices (and Blanks)", The Wilson Archives. Original Hexany papers showing different facets and configurations, not assembled by Erv Wilson (1967 on)
- "The Wilson Archives", Anaphoria.com
- "Hexany", RobertInventor.com. With a hexany you can turn around and click on any of its vertices, edges, or faces to hear the chords.
- "Combination-Product Set Patterns", Xenharmonikon IX (1986) by Kraig Grady.
- "Eikosany Papers", Anaphoria.com.
- "Musical Geometry", Music and Virtual Flowers. Intro. to musical geometry.
- "Alicia Boole Stott", The MacTutor History of Mathematics archive. Biography of Alicia Stott
- "The Tumbling Dekany", "Unusual musical scales", Dave Keenan's Home Page. Dave Keenan's Dekany tumbling in 4 dimensions — as a musical Excel spreadsheet
Musical tunings Measurement Just intonation Euler–Fokker genus · Harmonic Scale · Harry Partch's 43-tone scale · Hexany · Pythagorean tuning · Scale of harmonicsTemperaments IrregularTraditional non-Western Chinese musicology · Dastgah · Maqam (Arabian maqam · Makam · Mugham · Muqam) · Octoechos · Pelog · Raga (Carnatic rāga) · Slendro · TetrachordNon-octave Categories:- Multi-dimensional geometry
- Just tunings
- Musical scales
Wikimedia Foundation. 2010.