- Standard error (statistics)
-
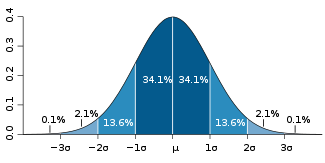 For a value that is sampled with an unbiased normally distributed error, the above depicts the proportion of samples that would fall between 0, 1, 2, and 3 standard deviations above and below the actual value.
For a value that is sampled with an unbiased normally distributed error, the above depicts the proportion of samples that would fall between 0, 1, 2, and 3 standard deviations above and below the actual value.
The standard error is the standard deviation of the sampling distribution of a statistic.[1] The term may also be used to refer to an estimate of that standard deviation, derived from a particular sample used to compute the estimate.
For example, the sample mean is the usual estimator of a population mean. However, different samples drawn from that same population would in general have different values of the sample mean. The standard error of the mean (i.e., of using the sample mean as a method of estimating the population mean) is the standard deviation of those sample means over all possible samples (of a given size) drawn from the population. Secondly, the standard error of the mean can refer to an estimate of that standard deviation, computed from the sample of data being analyzed at the time.
A way for remembering the term standard error is that, as long as the estimator is unbiased, the standard deviation of the error (the difference between the estimate and the true value) is the same as the standard deviation of the estimates themselves; this is true since the standard deviation of the difference between the random variable and its expected value is equal to the standard deviation of a random variable itself.
In practical applications, the true value of the standard deviation (of the error) is usually unknown. As a result, the term standard error is often used to refer to an estimate of this unknown quantity. In such cases it is important to be clear about what has been done and to attempt to take proper account of the fact that the standard error is only an estimate. Unfortunately, this is not often possible and it may then be better to use an approach that avoids using a standard error, for example by using maximum likelihood or a more formal approach to deriving confidence intervals. One well-known case where a proper allowance can be made arises where Student's t-distribution is used to provide a confidence interval for an estimated mean or difference of means. In other cases, the standard error may usefully be used to provide an indication of the size of the uncertainty, but its formal or semi-formal use to provide confidence intervals or tests should be avoided unless the sample size is at least moderately large. Here "large enough" would depend on the particular quantities being analyzed (see power).
In regression analysis, the term "standard error" is also used in the phrase standard error of the regression to mean the ordinary least squares estimate of the standard deviation of the underlying errors.[2][3]
Contents
Standard error of the mean
Further information: Variance#Sum of uncorrelated variables (Bienaymé formula)The standard error of the mean (SEM) is the standard deviation of the sample mean estimate of a population mean. (It can also be viewed as the standard deviation of the error in the sample mean relative to the true mean, since the sample mean is an unbiased estimator.) SEM is usually estimated by the sample estimate of the population standard deviation (sample standard deviation) divided by the square root of the sample size (assuming statistical independence of the values in the sample):
where
- s is the sample standard deviation (i.e., the sample-based estimate of the standard deviation of the population), and
- n is the size (number of observations) of the sample.
This estimate may be compared with the formula for the true standard deviation of the sample mean:
where
- σ is the standard deviation of the population.
This formula may be derived from what we know about the variance of a sum of independent random variables.[4]
- If X1, X2, ..., Xn are n independent observations from a population that has a mean μ and standard deviation σ, then the variance of the total T = (X1 + X2 + ... + Xn) is nσ2.
- The variance of T / n must be
 .
. - And the standard deviation of T / n must be
 .
. - Of course, T / n is the sample mean
 .
.
Note: the standard error and the standard deviation of small samples tend to systematically underestimate the population standard error and deviations: the standard error of the mean is a biased estimator of the population standard error. With n = 2 the underestimate is about 25%, but for n = 6 the underestimate is only 5%. Gurland and Tripathi (1971)[5] provide a correction and equation for this effect. Sokal and Rohlf (1981)[6] give an equation of the correction factor for small samples of n < 20. See unbiased estimation of standard deviation for further discussion.
A practical result: Decreasing the uncertainty in a mean value estimate by a factor of two requires acquiring four times as many observations in the sample. Or decreasing standard error by a factor of ten requires a hundred times as many observations.
Assumptions and usage
If the data are assumed to be normally distributed, quantiles of the normal distribution and the sample mean and standard error can be used to calculate approximate confidence intervals for the mean. The following expressions can be used to calculate the upper and lower 95% confidence limits, where
 is equal to the sample mean, SE is equal to the standard error for the sample mean, and 1.96 is the .975 quantile of the normal distribution:
is equal to the sample mean, SE is equal to the standard error for the sample mean, and 1.96 is the .975 quantile of the normal distribution:- Upper 95% Limit =

- Lower 95% Limit =

In particular, the standard error of a sample statistic (such as sample mean) is the estimated standard deviation of the error in the process by which it was generated. In other words, it is the standard deviation of the sampling distribution of the sample statistic. The notation for standard error can be any one of SE, SEM (for standard error of measurement or mean), or SE.
Standard errors provide simple measures of uncertainty in a value and are often used because:
- If the standard error of several individual quantities is known then the standard error of some function of the quantities can be easily calculated in many cases;
- Where the probability distribution of the value is known, it can be used to calculate a good approximation to an exact confidence interval; and
- Where the probability distribution is unknown, relationships like Chebyshev's or the Vysochanskiï-Petunin inequality can be used to calculate a conservative confidence interval
- As the sample size tends to infinity the central limit theorem guarantees that the sampling distribution of the mean is asymptotically normal.
Correction for finite population
The formula given above for the standard error assumes that the sample size is much smaller than the population size, so that the population can be considered to be effectively infinite in size. When the sampling fraction is large (approximately at 5% or more), the estimate of the error must be corrected by multiplying by a "finite population correction"[7]
to account for the added precision gained by sampling close to a larger percentage of the population. The effect of the FPC is that the error becomes zero when the sample size n is equal to the population size N.
Correction for correlation in the sample
If values of the measured quantity A are not statistically independent but have been obtained from known locations in parameter space x, an unbiased estimate of the true standard error of the mean (actually a correction on the standard deviation part) may be obtained by multiplying the calculated standard error of the sample by the factor f:
where the sample bias coefficient ρ is the widely used Prais-Winsten estimate of the autocorrelation-coefficient (a quantity between -1 and 1) for all sample point pairs. This approximate formula is for moderate to large sample sizes; the reference gives the exact formulas for any sample size, and can be applied to heavily autocorrelated time series like Wall Street stock quotes. Moreover this formula works for positive and negative ρ alike.[8] See also unbiased estimation of standard deviation for more discussion.
Relative standard error
The relative standard error (RSE) is simply the standard error divided by the mean and expressed as a percentage. For example, consider two surveys of household income that both result in a sample mean of $50,000. If one survey has a standard error of $10,000 and the other has a standard error of $5,000, then the relative standard errors are 20% and 10% respectively. The survey with the lower relative standard error has a more precise measurement since there is less variance around the mean. In fact, data organizations often set reliability standards that their data must reach before publication. For example, the U.S. National Center for Health Statistics typically does not report an estimate if the relative standard error exceeds 30%. (NCHS also typically requires at least 30 observations for an estimate to be reported.)[citation needed]
See also
- Probable error
- Variance
- Sample mean and sample covariance
References
- ^ Everitt, B.S. (2003) The Cambridge Dictionary of Statistics, CUP. ISBN 0-521-81099-x
- ^ Kenney, J. and Keeping, E.S. (1963) Mathematics of Statistics, van Nostrand, p. 187
- ^ Zwillinger D. (1995), Standard Mathematical Tables and Formulae, Chapman&Hall/CRC. ISBN 0849324793 p. 626
- ^ T.P. Hutchinson, Essentials of statistical methods in 41 pages
- ^ Gurland, J; Tripathi RC (1971). "A simple approximation for unbiased estimation of the standard deviation". American Statistician (American Statistical Association) 25 (4): 30–32. doi:10.2307/2682923. JSTOR 2682923.
- ^ Sokal and Rohlf (1981) Biometry: Principles and Practice of Statistics in Biological Research , 2nd ed.. ISBN 0716712547 , p 53
- ^ Isserlis, L. (1918). "On the value of a mean as calculated from a sample". Journal of the Royal Statistical Society (Blackwell Publishing) 81 (1): 75–81. doi:10.2307/2340569. JSTOR 2340569. (Equation 1)
- ^ James R. Bence (1995) Analysis of short time series: Correcting for autocorrelation. Ecology 76(2): 628 – 639.
Categories:- Statistical deviation and dispersion
Wikimedia Foundation. 2010.





