- Cross product
-
This article is about the cross product of two vectors in three-dimensional Euclidean space. For other uses, see Cross product (disambiguation).
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them. The name is derived from the cross symbol "×" that is often used to designate this operation; the alternative name vector product emphasizes the vector (rather than scalar) nature of the result. It has many applications in mathematics, engineering and physics.
If either of the vectors being multiplied is zero or the vectors are parallel then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular for perpendicular vectors this is a rectangle and the magnitude of the product is the product of their lengths. The cross product is anticommutative, distributive over addition and satisfies the Jacobi identity. The space and product form an algebra over a field, which is neither commutative nor associative, but is a Lie algebra with the cross product being the Lie bracket.
Like the dot product, it depends on the metric of Euclidean space, but unlike the dot product, it also depends on the choice of orientation or "handedness". The product can be generalized in various ways; it can be made independent of orientation by changing the result to pseudovector, or in arbitrary dimensions the exterior product of vectors can be used with a bivector or two-form result. Also, using the orientation and metric structure just as for the traditional 3-dimensional cross product, one can in n dimensions take the product of n − 1 vectors to produce a vector perpendicular to all of them. But if the product is limited to non-trivial binary products with vector results, it exists only in three and seven dimensions.[citation needed]
Contents
Definition
 Finding the direction of the cross product by the right-hand rule
Finding the direction of the cross product by the right-hand rule
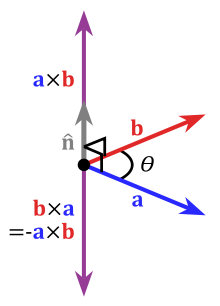
The cross product of two vectors a and b is denoted by a × b. In physics, sometimes the notation a ∧ b is used,[1] though this is avoided in mathematics to avoid confusion with the exterior product.
The cross product a × b is defined as a vector c that is perpendicular to both a and b, with a direction given by the right-hand rule and a magnitude equal to the area of the parallelogram that the vectors span.
The cross product is defined by the formula[2][3]
where θ is the measure of the smaller angle between a and b (0° ≤ θ ≤ 180°), a and b are the magnitudes of vectors a and b (i.e., a = |a| and b = |b|), and n is a unit vector perpendicular to the plane containing a and b in the direction given by the right-hand rule as illustrated. If the vectors a and b are parallel (i.e., the angle θ between them is either 0° or 180°), by the above formula, the cross product of a and b is the zero vector 0.
The direction of the vector n is given by the right-hand rule, where one simply points the forefinger of the right hand in the direction of a and the middle finger in the direction of b. Then, the vector n is coming out of the thumb (see the picture on the right). Using this rule implies that the cross-product is anti-commutative, i.e., b × a = −(a × b). By pointing the forefinger toward b first, and then pointing the middle finger toward a, the thumb will be forced in the opposite direction, reversing the sign of the product vector.
Using the cross product requires the handedness of the coordinate system to be taken into account (as explicit in the definition above). If a left-handed coordinate system is used, the direction of the vector n is given by the left-hand rule and points in the opposite direction.
This, however, creates a problem because transforming from one arbitrary reference system to another (e.g., a mirror image transformation from a right-handed to a left-handed coordinate system), should not change the direction of n. The problem is clarified by realizing that the cross-product of two vectors is not a (true) vector, but rather a pseudovector. See cross product and handedness for more detail.
Computing the cross product
Coordinate notation
The standard basis vectors i, j, and k satisfy the following equalities:
Together with the skew-symmetry and bilinearity of the product, these three identities are sufficient to determine the cross product of any two vectors. In particular, the following identities can be established:

 (the zero vector)
(the zero vector)
These can be used to compute the product of two general vectors, a = a1i + a2j + a3k and b = b1i + b2j + b3k, by expanding the product using distributivity then collecting similar terms:
Or written as column vectors:
Matrix notation
The definition of the cross product can also be represented by the determinant of a formal matrix:
This determinant can be computed using Sarrus' rule or Cofactor expansion.
Using Sarrus' Rule, it expands to
Using Cofactor expansion along the first row instead, it expands to[4]
which gives the components of the resulting vector directly.
An elegant, alternative derivation is based on an isometric sketch of (x,y,z) axes with the (x,y,z) components of each vector (A,B) drawn parallel to the corresponding axes. The resulting formula for the constituents of the cross product (C = A x B) then appears by inspection, provided we are careful to take all orthogonal cross products in the order A:B (such as Az x Bx). For example, this method yields the magnitude (Cz = AxBy - AyBx) for the vector component along the z-axis and unit vector (k).
Properties
Geometric meaning
See also: Triple productThe magnitude of the cross product can be interpreted as the positive area of the parallelogram having a and b as sides (see Figure 1):
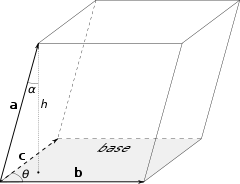
Indeed, one can also compute the volume V of a parallelepiped having a, b and c as sides by using a combination of a cross product and a dot product, called scalar triple product (see Figure 2):
Since the result of the scalar triple product may be negative, the volume of the parallelepiped is given by its absolute value. For instance,
Because the magnitude of the cross product goes by the sine of the angle between its arguments, the cross product can be thought of as a measure of "perpendicularness" in the same way that the dot product is a measure of "parallelness". Given two unit vectors, their cross product has a magnitude of 1 if the two are perpendicular and a magnitude of zero if the two are parallel. The opposite is true for the dot product of two unit vectors.
Unit vectors enable two convenient identities: the dot product of two unit vectors yields the cosine (which may be positive or negative) of the angle between the two unit vectors. The magnitude of the cross product of the two unit vectors yields the sine (which will always be positive).
Algebraic properties
The cross product is anticommutative,
distributive over addition,
and compatible with scalar multiplication so that
It is not associative, but satisfies the Jacobi identity:
Distributivity, linearity and Jacobi identity show that R3 together with vector addition and the cross product forms a Lie algebra, the Lie algebra of the real orthogonal group in 3 dimensions, SO(3).
The cross product does not obey the cancellation law: a × b = a × c with non-zero a does not imply that b = c. Instead if a × b = a × c:
If neither a nor b - c is zero then from the definition of the cross product the angle between them must be zero and they must be parallel. They are related by a scale factor, so one of b or c can be expressed in terms of the other, for example
for some scalar t.
If a · b = a · c and a × b = a × c, for non-zero vector a, then b = c, as
 and
and
so b − c is both parallel and perpendicular to the non-zero vector a, something that is only possible if b − c = 0 so they are identical.
From the geometrical definition the cross product is invariant under rotations about the axis defined by a × b. More generally the cross product obeys the following identity under matrix transformations:
where
 is a 3 by 3 matrix and
is a 3 by 3 matrix and  is the transpose of the inverse
is the transpose of the inverseThe cross product of two vectors in 3-D always lies in the null space of the matrix with the vectors as rows:
For the sum of two cross products, the following identity holds:
Differentiation
The product rule applies to the cross product in a similar manner:
This identity can be easily proved using the matrix multiplication representation.
Triple product expansion
Main article: Triple productThe cross product is used in both forms of the triple product. The scalar triple product of three vectors is defined as
It is the signed volume of the parallelepiped with edges a, b and c and as such the vectors can be used in any order that's an even permutation of the above ordering. The following therefore are equal:
The vector triple product is the cross product of a vector with the result of another cross product, and is related to the dot product by the following formula
The mnemonic "BAC minus CAB" is used to remember the order of the vectors in the right hand member. This formula is used in physics to simplify vector calculations. A special case, regarding gradients and useful in vector calculus, is
where ∇2 is the vector Laplacian operator.
Another identity relates the cross product to the scalar triple product:
Alternative formulation
The cross product and the dot product are related by:
The right-hand side is the Gram determinant of a and b, the square of the area of the parallelogram defined by the vectors. This condition determines the magnitude of the cross product. Namely, since the dot product is defined, in terms of the angle θ between the two vectors, as:
the above given relationship can be rewritten as follows:
Invoking the Pythagorean trigonometric identity one obtains:
which is the magnitude of the cross product expressed in terms of θ, equal to the area of the parallelogram defined by a and b (see definition above).
The combination of this requirement and the property that the cross product be orthogonal to its constituents a and b provides an alternative definition of the cross product.[5]
Lagrange's identity
The relation:
can be compared with another relation involving the right-hand side, namely Lagrange's identity expressed as:[6]
where a and b may be n-dimensional vectors. In the case n=3, combining these two equations results in the expression for the magnitude of the cross product in terms of its components:[7]
The same result is found directly using the components of the cross-product found from:
In R3 Lagrange's equation is a special case of the multiplicativity |vw| = |v||w| of the norm in the quaternion algebra.
It is a special case of another formula, also sometimes called Lagrange's identity, which is the three dimensional case of the Binet-Cauchy identity:[8][9]
If a = c and b = d this simplifies to the formula above.
Alternative ways to compute the cross product
Conversion to matrix multiplication
The vector cross product also can be expressed as the product of a skew-symmetric matrix and a vector:[8]
where superscript T refers to the Transpose matrix, and [a]× is defined by:
Also, if a is itself a cross product:
then[citation needed]
This result can be generalized to higher dimensions using geometric algebra. In particular in any dimension bivectors can be identified with skew-symmetric matrices, so the product between a skew-symmetric matrix and vector is equivalent to the grade-1 part of the product of a bivector and vector.[citation needed] In three dimensions bivectors are dual to vectors so the product is equivalent to the cross product, with the bivector instead of its vector dual. In higher dimensions the product can still be calculated but bivectors have more degrees of freedom and are not equivalent to vectors.[citation needed]
This notation is also often much easier to work with, for example, in epipolar geometry.
From the general properties of the cross product follows immediately that
![[\mathbf{a}]_{\times} \, \mathbf{a} = \mathbf{0}](1/301010a6bc8c3118385f05faf41d8219.png) and
and ![\mathbf{a}^\mathrm T \, [\mathbf{a}]_{\times} = \mathbf{0}](1/a51d904263600d1604cf9c71f4c327d3.png)
and from fact that [a]× is skew-symmetric it follows that
The above-mentioned triple product expansion (bac-cab rule) can be easily proven using this notation.[citation needed]
The above definition of [a]× means that there is a one-to-one mapping between the set of 3×3 skew-symmetric matrices, also known as the Lie algebra of SO(3), and the operation of taking the cross product with some vector a.[citation needed]
Index notation
The cross product can alternatively be defined in terms of the Levi-Civita symbol, εijk:
where the indices
 correspond, as in the previous section, to orthogonal vector components. This characterization of the cross product is often expressed more compactly using the Einstein summation convention as
correspond, as in the previous section, to orthogonal vector components. This characterization of the cross product is often expressed more compactly using the Einstein summation convention asin which repeated indices are summed from 1 to 3. Note that this representation is another form of the skew-symmetric representation of the cross product:
In classical mechanics: representing the cross-product with the Levi-Civita symbol can cause mechanical-symmetries to be obvious when physical-systems are isotropic in space. (Quick example: consider a particle in a Hooke's Law potential in three-space, free to oscillate in three dimensions; none of these dimensions are "special" in any sense, so symmetries lie in the cross-product-represented angular-momentum which are made clear by the abovementioned Levi-Civita representation).[citation needed]
Mnemonic
The word "xyzzy" can be used to remember the definition of the cross product.
If
where:
then:
The second and third equations can be obtained from the first by simply vertically rotating the subscripts, x → y → z → x. The problem, of course, is how to remember the first equation, and two options are available for this purpose: either to remember the relevant two diagonals of Sarrus's scheme (those containing i), or to remember the xyzzy sequence.
Since the first diagonal in Sarrus's scheme is just the main diagonal of the above-mentioned
 matrix, the first three letters of the word xyzzy can be very easily remembered.
matrix, the first three letters of the word xyzzy can be very easily remembered.Cross Visualization
Similarly to the mnemonic device above, a "cross" or X can be visualized between the two vectors in the equation. This may help you to remember the correct cross product formula.
If
then:
If we want to obtain the formula for ax we simply drop the bx and cx from the formula, and take the next two components down -
It should be noted that when doing this for ay the next two elements down should "wrap around" the matrix so that after the z component comes the x component. For clarity, when performing this operation for ay, the next two components should be z and x (in that order). While for az the next two components should be taken as x and y.
For ax then, if we visualize the cross operator as pointing from an element on the left to an element on the right, we can take the first element on the left and simply multiply by the element that the cross points to in the right hand matrix. We then subtract the next element down on the left, multiplied by the element that the cross points to here as well. This results in our ax formula -
We can do this in the same way for ay and az to construct their associated formulas.
Applications
Computational geometry
The cross product can be used to calculate the normal for a triangle or polygon, an operation frequently performed in computer graphics. For example, the winding of polygon (clockwise or anticlockwise) about a point within the polygon (i.e. the centroid or mid-point) can be calculated by triangulating the polygon (like spoking a wheel) and summing the angles (between the spokes) using the cross product to keep track of the sign of each angle.
In computational geometry of the plane, the cross product is used to determine the sign of the acute angle defined by three points ,
,  and
and  . It corresponds to the direction of the cross product of the two coplanar vectors defined by the pairs of points
. It corresponds to the direction of the cross product of the two coplanar vectors defined by the pairs of points  and
and  , i.e., by the sign of the expression
, i.e., by the sign of the expression  . In the "right-handed" coordinate system, if the result is 0, the points are collinear; if it is positive, the three points constitute a negative angle of rotation around
. In the "right-handed" coordinate system, if the result is 0, the points are collinear; if it is positive, the three points constitute a negative angle of rotation around  from
from  to
to  , otherwise a positive angle. From another point of view, the sign of
, otherwise a positive angle. From another point of view, the sign of  tells whether
tells whether  lies to the left or to the right of line
lies to the left or to the right of line  .
.Mechanics
Moment of a force
 applied at point B around point A is given as:
applied at point B around point A is given as:Other
The cross product occurs in the formula for the vector operator curl. It is also used to describe the Lorentz force experienced by a moving electrical charge in a magnetic field. The definitions of torque and angular momentum also involve the cross product.
The trick of rewriting a cross product in terms of a matrix multiplication appears frequently in epipolar and multi-view geometry, in particular when deriving matching constraints.
Cross product as an exterior product
 The cross product in relation to the exterior product. In red are the orthogonal unit vector, and the "parallel" unit bivector.
The cross product in relation to the exterior product. In red are the orthogonal unit vector, and the "parallel" unit bivector.
The cross product can be viewed in terms of the exterior product. This view allows for a natural geometric interpretation of the cross product. In exterior calculus the exterior product (or wedge product) of two vectors is a bivector. A bivector is an oriented plane element, in much the same way that a vector is an oriented line element. Given two vectors a and b, one can view the bivector a∧b as the oriented parallelogram spanned by a and b. The cross product is then obtained by taking the Hodge dual of the bivector a∧b, identifying 2-vectors with vectors:
This can be thought of as the oriented multi-dimensional element "perpendicular" to the bivector. Only in three dimensions is the result an oriented line element – a vector – whereas, for example, in 4 dimensions the Hodge dual of a bivector is two-dimensional – another oriented plane element. So, only in three dimensions is the cross product of a and b the vector dual to the bivector a∧b: it is perpendicular to the bivector, with orientation dependent on the coordinate system's handedness, and has the same magnitude relative to the unit normal vector as a∧b has relative to the unit bivector; precisely the properties described above.
Cross product and handedness
When measurable quantities involve cross products, the handedness of the coordinate systems used cannot be arbitrary. However, when physics laws are written as equations, it should be possible to make an arbitrary choice of the coordinate system (including handedness). To avoid problems, one should be careful to never write down an equation where the two sides do not behave equally under all transformations that need to be considered. For example, if one side of the equation is a cross product of two vectors, one must take into account that when the handedness of the coordinate system is not fixed a priori, the result is not a (true) vector but a pseudovector. Therefore, for consistency, the other side must also be a pseudovector.[citation needed]
More generally, the result of a cross product may be either a vector or a pseudovector, depending on the type of its operands (vectors or pseudovectors). Namely, vectors and pseudovectors are interrelated in the following ways under application of the cross product:
- vector × vector = pseudovector
- pseudovector × pseudovector = pseudovector
- vector × pseudovector = vector
- pseudovector × vector = vector.
So by the above relationships, the unit basis vectors i, j and k of an orthonormal, right-handed (Cartesian) coordinate frame must all be pseudovectors (if a basis of mixed vector types is disallowed, as it normally is) since i × j = k, j × k = i and k × i = j.
Because the cross product may also be a (true) vector, it may not change direction with a mirror image transformation. This happens, according to the above relationships, if one of the operands is a (true) vector and the other one is a pseudovector (e.g., the cross product of two vectors). For instance, a vector triple product involving three (true) vectors is a (true) vector.
A handedness-free approach is possible using exterior algebra.
Generalizations
There are several ways to generalize the cross product to the higher dimensions.
Lie algebra
Main article: Lie algebraThe cross product can be seen as one of the simplest Lie products, and is thus generalized by Lie algebras, which are axiomatized as binary products satisfying the axioms of multilinearity, skew-symmetry, and the Jacobi identity. Many Lie algebras exist, and their study is a major field of mathematics, called Lie theory.
For example, the Heisenberg algebra gives another Lie algebra structure on
 In the basis
In the basis  the product is
the product is ![\scriptstyle [x,y]=z, [x,z]=[y,z]=0.](b/e8b8085b8d76d917a57390a4557778a3.png)
Quaternions
Further information: quaternions and spatial rotationThe cross product can also be described in terms of quaternions, and this is why the letters i, j, k are a convention for the standard basis on
 . The unit vectors i, j, k correspond to "binary" (180 deg) rotations about their respective axes (Altmann, S. L., 1986, Ch. 12), said rotations being represented by "pure" quaternions (zero scalar part) with unit norms.
. The unit vectors i, j, k correspond to "binary" (180 deg) rotations about their respective axes (Altmann, S. L., 1986, Ch. 12), said rotations being represented by "pure" quaternions (zero scalar part) with unit norms.For instance, the above given cross product relations among i, j, and k agree with the multiplicative relations among the quaternions i, j, and k. In general, if a vector [a1, a2, a3] is represented as the quaternion a1i + a2j + a3k, the cross product of two vectors can be obtained by taking their product as quaternions and deleting the real part of the result. The real part will be the negative of the dot product of the two vectors.
Alternatively and more straightforwardly, using the above identification of the 'purely imaginary' quaternions with
 , the cross product may be thought of as half of the commutator of two quaternions.
, the cross product may be thought of as half of the commutator of two quaternions.Octonions
See also: Seven-dimensional cross product and OctonionA cross product for 7-dimensional vectors can be obtained in the same way by using the octonions instead of the quaternions. The nonexistence of such cross products of two vectors in other dimensions is related to the result that the only normed division algebras are the ones with dimension 1, 2, 4, and 8; Hurwitz's theorem.
Wedge product
Main article: Exterior algebraIn general dimension, there is no direct analogue of the binary cross product. There is however the wedge product, which has similar properties, except that the wedge product of two vectors is now a 2-vector instead of an ordinary vector. As mentioned above, the cross product can be interpreted as the wedge product in three dimensions after using Hodge duality to identify 2-vectors with vectors.
The wedge product and dot product can be combined to form the Clifford product.
Multilinear algebra
In the context of multilinear algebra, the cross product can be seen as the (1,2)-tensor (a mixed tensor, specifically a bilinear map) obtained from the 3-dimensional volume form,[note 1] a (0,3)-tensor, by raising an index.
In detail, the 3-dimensional volume form defines a product
 by taking the determinant of the matrix given by these 3 vectors. By duality, this is equivalent to a function
by taking the determinant of the matrix given by these 3 vectors. By duality, this is equivalent to a function  (fixing any two inputs gives a function
(fixing any two inputs gives a function  by evaluating on the third input) and in the presence of an inner product (such as the dot product; more generally, a non-degenerate bilinear form), we have an isomorphism
by evaluating on the third input) and in the presence of an inner product (such as the dot product; more generally, a non-degenerate bilinear form), we have an isomorphism  and thus this yields a map
and thus this yields a map  which is the cross product: a (0,3)-tensor (3 vector inputs, scalar output) has been transformed into a (1,2)-tensor (2 vector inputs, 1 vector output) by "raising an index".
which is the cross product: a (0,3)-tensor (3 vector inputs, scalar output) has been transformed into a (1,2)-tensor (2 vector inputs, 1 vector output) by "raising an index".Translating the above algebra into geometry, the function "volume of the parallelepiped defined by
 " (where the first two vectors are fixed and the last is an input), which defines a function
" (where the first two vectors are fixed and the last is an input), which defines a function  , can be represented uniquely as the dot product with a vector: this vector is the cross product
, can be represented uniquely as the dot product with a vector: this vector is the cross product  From this perspective, the cross product is defined by the scalar triple product,
From this perspective, the cross product is defined by the scalar triple product, 
In the same way, in higher dimensions one may define generalized cross products by raising indices of the n-dimensional volume form, which is a
 -tensor. The most direct generalizations of the cross product are to define either:
-tensor. The most direct generalizations of the cross product are to define either:- a
 -tensor, which takes as input
-tensor, which takes as input  vectors, and gives as output 1 vector – an
vectors, and gives as output 1 vector – an  -ary vector-valued product, or
-ary vector-valued product, or - a
 -tensor, which takes as input 2 vectors and gives as output skew-symmetric tensor of rank n−2 – a binary product with rank n−2 tensor values. One can also define
-tensor, which takes as input 2 vectors and gives as output skew-symmetric tensor of rank n−2 – a binary product with rank n−2 tensor values. One can also define  -tensors for other k.
-tensors for other k.
These products are all multilinear and skew-symmetric, and can be defined in terms of the determinant and parity.
The
 -ary product can be described as follows: given
-ary product can be described as follows: given  vectors
vectors  in
in  define their generalized cross product
define their generalized cross product  as:
as:- perpendicular to the hyperplane defined by the

- magnitude is the volume of the parallelotope defined by the
 which can be computed as the Gram determinant of the
which can be computed as the Gram determinant of the 
- oriented so that
 is positively oriented.
is positively oriented.
This is the unique multilinear, alternating product which evaluates to
 ,
,  and so forth for cyclic permutations of indices.
and so forth for cyclic permutations of indices.In coordinates, one can give a formula for this
 -ary analogue of the cross product in Rn by:
-ary analogue of the cross product in Rn by:This formula is identical in structure to the determinant formula for the normal cross product in R3 except that the row of basis vectors is the last row in the determinant rather than the first. The reason for this is to ensure that the ordered vectors (v1,...,vn-1,Λ(v1,...,vn-1)) have a positive orientation with respect to (e1,...,en). If n is odd, this modification leaves the value unchanged, so this convention agrees with the normal definition of the binary product. In the case that n is even, however, the distinction must be kept. This
 -ary form enjoys many of the same properties as the vector cross product: it is alternating and linear in its arguments, it is perpendicular to each argument, and its magnitude gives the hypervolume of the region bounded by the arguments. And just like the vector cross product, it can be defined in a coordinate independent way as the Hodge dual of the wedge product of the arguments.
-ary form enjoys many of the same properties as the vector cross product: it is alternating and linear in its arguments, it is perpendicular to each argument, and its magnitude gives the hypervolume of the region bounded by the arguments. And just like the vector cross product, it can be defined in a coordinate independent way as the Hodge dual of the wedge product of the arguments.History
In 1773, Joseph Louis Lagrange introduced the component form of both the dot and cross products in order to study the tetrahedron in three dimensions.[10] In 1843 the Irish mathematical physicist Sir William Rowan Hamilton introduced the quaternion product, and with it the terms "vector" and "scalar". Given two quaternions [0, u] and [0, v], where u and v are vectors in R3, their quaternion product can be summarized as [−u·v, u×v]. James Clerk Maxwell used Hamilton's quaternion tools to develop his famous electromagnetism equations, and for this and other reasons quaternions for a time were an essential part of physics education.
In 1878 William Kingdon Clifford published his Elements of Dynamic which was an advanced text for its time. He defined the product of two vectors[11] to have magnitude equal to the area of the parallelogram of which they are two sides, and direction perpendicular to their plane.
Oliver Heaviside in England and Josiah Willard Gibbs, a professor at Yale University in Connecticut, also felt that quaternion methods were too cumbersome, often requiring the scalar or vector part of a result to be extracted. Thus, about forty years after the quaternion product, the dot product and cross product were introduced—to heated opposition. Pivotal to (eventual) acceptance was the efficiency of the new approach, allowing Heaviside to reduce the equations of electromagnetism from Maxwell's original 20 to the four commonly seen today.[12]
Largely independent of this development, and largely unappreciated at the time, Hermann Grassmann created a geometric algebra not tied to dimension two or three, with the exterior product playing a central role. William Kingdon Clifford combined the algebras of Hamilton and Grassmann to produce Clifford algebra, where in the case of three-dimensional vectors the bivector produced from two vectors dualizes to a vector, thus reproducing the cross product.
The cross notation, which began with Gibbs, inspired the name "cross product". Originally it appeared in privately published notes for his students in 1881 as Elements of Vector Analysis. The utility for mechanics was noted by Aleksandr Kotelnikov. Gibbs's notation —and the name— later reached a wide audience through Vector Analysis, a textbook by Edwin Bidwell Wilson, a former student. Wilson rearranged material from Gibbs's lectures, together with material from publications by Heaviside, Föpps, and Hamilton. He divided vector analysis into three parts:
First, that which concerns addition and the scalar and vector products of vectors. Second, that which concerns the differential and integral calculus in its relations to scalar and vector functions. Third, that which contains the theory of the linear vector function.Two main kinds of vector multiplications were defined, and they were called as follows:
- The direct, scalar, or dot product of two vectors
- The skew, vector, or cross product of two vectors
Several kinds of triple products and products of more than three vectors were also examined. The above mentioned triple product expansion was also included.
See also
- Multiple cross products – Products involving more than three vectors
- Cartesian product – A product of two sets
- × (the symbol)
- Bivector
- Pseudovector
Notes
- ^ By a volume form one means a function that takes in n vectors and gives out a scalar, the volume of the parallelotope defined by the vectors:
 This is an n-ary multilinear skew-symmetric form. In the presence of a basis, such as on
This is an n-ary multilinear skew-symmetric form. In the presence of a basis, such as on  this is given by the determinant, but in an abstract vector space, this is added structure. In terms of G-structures, a volume form is an
this is given by the determinant, but in an abstract vector space, this is added structure. In terms of G-structures, a volume form is an  -structure.
-structure.
References
- ^ Jeffreys, H and Jeffreys, BS (1999). Methods of mathematical physics. Cambridge University Press. http://worldcat.org/oclc/41158050?tab=details.
- ^ Wilson 1901, p. 60–61
- ^ Dennis G. Zill, Michael R. Cullen (2006). "Definition 7.4: Cross product of two vectors". Advanced engineering mathematics (3rd ed.). Jones & Bartlett Learning. p. 324. ISBN 076374591X. http://books.google.com/?id=x7uWk8lxVNYC&pg=PA324.
- ^ Dennis G. Zill, Michael R. Cullen (2006). "Equation 7: a × b as sum of determinants". cited work. Jones & Bartlett Learning. p. 321. ISBN 076374591X. http://books.google.com/?id=x7uWk8lxVNYC&pg=PA321.
- ^ WS Massey (Dec. 1983). "Cross products of vectors in higher dimensional Euclidean spaces". The American Mathematical Monthly (The American Mathematical Monthly, Vol. 90, No. 10) 90 (10): 697–701. doi:10.2307/2323537. JSTOR 2323537.
- ^ Vladimir A. Boichenko, Gennadiĭ Alekseevich Leonov, Volker Reitmann (2005). Dimension theory for ordinary differential equations. Vieweg+Teubner Verlag. p. 26. ISBN 3519004372. http://books.google.com/?id=9bN1-b_dSYsC&pg=PA26.
- ^ Pertti Lounesto (2001). Clifford algebras and spinors (2nd ed.). Cambridge University Press. p. 94. ISBN 0521005515. http://books.google.com/?id=kOsybQWDK4oC&pg=PA94&dq=%22which+in+coordinate+form+means+Lagrange%27s+identity%22&cd=1#v=onepage&q=%22which%20in%20coordinate%20form%20means%20Lagrange%27s%20identity%22.
- ^ a b Shuangzhe Liu and Gõtz Trenkler (2008). "Hadamard, Khatri-Rao, Kronecker and other matrix products". Int J Information and systems sciences (Institute for scientific computing and education) 4 (1): 160–177. http://www.math.ualberta.ca/ijiss/SS-Volume-4-2008/No-1-08/SS-08-01-17.pdf.
- ^ by Eric W. Weisstein (2003). "Binet-Cauchy identity". CRC concise encyclopedia of mathematics (2nd ed.). CRC Press. p. 228. ISBN 1584883472. http://books.google.com/?id=8LmCzWQYh_UC&pg=PA228.
- ^ Lagrange, JL (1773). "Solutions analytiques de quelques problèmes sur les pyramides triangulaires". Oeuvres. vol 3.
- ^ William Kingdon Clifford (1878) Elements of Dynamic, Part I, page 95, London: MacMillan & Co; online presentation by Cornell University Historical Mathematical Monographs
- ^ Nahin, Paul J. (2000). Oliver Heaviside: the life, work, and times of an electrical genius of the Victorian age. JHU Press. pp. 108–109. ISBN 0-801-86909-9.
- Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing. p. 134. ISBN 978-0-486-67766-8. http://www.archive.org/details/historyofmathema027671mbp
- E. A. Milne (1948) Vectorial Mechanics, Chapter 2: Vector Product, pp 11 –31, London: Methuen Publishing.
- Wilson, Edwin Bidwell (1901). Vector Analysis: A text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs. Yale University Press. http://www.archive.org/details/117714283
External links
- Weisstein, Eric W., "Cross Product" from MathWorld.
- A quick geometrical derivation and interpretation of cross products
- Z.K. Silagadze (2002). Multi-dimensional vector product. Journal of Physics. A35, 4949 (it is only possible in 7-D space)
- Real and Complex Products of Complex Numbers
- An interactive tutorial created at Syracuse University - (requires java)
- W. Kahan (2007). Cross-Products and Rotations in Euclidean 2- and 3-Space. University of California, Berkeley (PDF).
Topics related to linear algebra Scalar · Vector · Vector space · Vector projection · Linear span · Linear map · Linear projection · Linear independence · Linear combination · Basis · Column space · Row space · Dual space · Orthogonality · Rank · Minor · Kernel · Eigenvalues and eigenvectors · Least squares regressions · Outer product · Inner product space · Dot product · Transpose · Gram–Schmidt process · Matrix decompositionCategories:- Abstract algebra
- Bilinear operators
- Binary operations
- Vectors
- Vector calculus
- Multilinear algebra
- Analytic geometry
Wikimedia Foundation. 2010.



































![\mathbf{a} \times \mathbf{b} = [\mathbf{a}]_{\times} \mathbf{b} = \begin{bmatrix}\,0&\!-a_3&\,\,a_2\\ \,\,a_3&0&\!-a_1\\-a_2&\,\,a_1&\,0\end{bmatrix}\begin{bmatrix}b_1\\b_2\\b_3\end{bmatrix}](0/ca026774b80d5719b6470de839a17058.png)
![\mathbf{a} \times \mathbf{b} = [\mathbf{b}]_{\times}^\mathrm T \mathbf{a} = \begin{bmatrix}\,0&\,\,b_3&\!-b_2\\ -b_3&0&\,\,b_1\\\,\,b_2&\!-b_1&\,0\end{bmatrix}\begin{bmatrix}a_1\\a_2\\a_3\end{bmatrix}](9/e191fece1ec072a2233f4aeab51fce8e.png)
![[\mathbf{a}]_{\times} \stackrel{\rm def}{=} \begin{bmatrix}\,\,0&\!-a_3&\,\,\,a_2\\\,\,\,a_3&0&\!-a_1\\\!-a_2&\,\,a_1&\,\,0\end{bmatrix}.](2/ab2068bb3d2a5b2e681bea51e1de17f3.png)

![[\mathbf{a}]_{\times} = (\mathbf{c}\mathbf{d}^\mathrm T)^\mathrm T - \mathbf{c}\mathbf{d}^\mathrm T.](a/17ad86b58e6c659eb556448914f18d29.png)
![\mathbf{b}^\mathrm T \, [\mathbf{a}]_{\times} \, \mathbf{b} = 0.](3/793483492ba2325e65e9968add54af1a.png)


![\varepsilon_{ijk} a_j = [\mathbf{a}]_\times.](3/9e3e7eb28ed1a1bfa2c7e3a176de0c3d.png)











