- Angle
-
This article is about angles in geometry. For other uses, see Angle (disambiguation)."Oblique angle" redirects here. For the cinematographic technique, see Dutch angle.
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.[1] Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc. On another type of plane where a hyperbola provides the standard of direction, the measure of an interval on the hyperbola is called hyperbolic angle.
The word angle comes from the Latin word angulus, meaning "a corner". The word angulus is a diminutive, of which the primitive form, angus, does not occur in Latin. Cognate words are the Greek ἀγκύλος (ankylοs), meaning "crooked, curved," and the English word "ankle". Both are connected with the Proto-Indo-European root *ank-, meaning "to bend" or "bow".[2]
Euclid defines a plane angle as the inclination to each other, in a plane, of two lines which meet each other, and do not lie straight with respect to each other. According to Proclus an angle must be either a quality or a quantity, or a relationship. The first concept was used by Eudemus, who regarded an angle as a deviation from a straight line; the second by Carpus of Antioch, who regarded it as the interval or space between the intersecting lines; Euclid adopted the third concept, although his definitions of right, acute, and obtuse angles are certainly quantitative.[3]
Measuring angles
Two angles are sometimes called congruent if there exists an isometry that transforms one of the angles into the other angle. The size of an angle is normally characterized by the smallest positive rotation that maps one of the rays into the other. Two angles are congruent if and only if they correspond to the same (smallest positive) rotation. Thus an angle as two rays is characterized by an angle of rotation. To avoid confusion when no isometry exists between particular representations of angles, angles that Euclid called "equal" are described as "equal in measure".
In many geometrical situations, angles that differ by an exact multiple of a full circle are effectively equivalent (it makes no difference how many times a line is rotated through a full circle because it always ends up in the same place). However, this is not always the case. For example, when tracing a curve such as a spiral using polar coordinates, an extra full turn gives rise to a quite different point on the curve.
In order to measure an angle θ, a circular arc centered at the vertex of the angle is drawn, e.g. with a pair of compasses. The length of the arc s is then divided by the radius of the circle r, and possibly multiplied by a scaling constant k (which depends on the units of measurement that are chosen):
The value of θ thus defined is independent of the size of the circle: if the length of the radius is changed then the arc length changes in the same proportion, so the ratio s/r is unaltered.
Units
In dimensional analysis, angles are considered to be dimensionless. There are several units used to measure angles. Of these units, listed below according to magnitude, the degree and the radian are by far the most common.
Most units of angular measurement are defined such that one turn (i.e. one full circle) is equal to n units, for some whole number n. The two exceptions are the radian and the diameter part. For example, in the case of degrees, n = 360. A turn of n units is obtained by setting k = n/(2π) in the formula above. (Proof. The formula above can be rewritten as k = θr/s. One turn, for which θ = n units, corresponds to an arc equal in length to the circle's circumference, which is 2πr, so s = 2πr. Substituting n for θ and 2πr for s in the formula, results in k = nr/(2πr) = n/(2π).)
- The turn (or full circle, revolution, rotation, or cycle) is one full circle. A turn can be subdivided in centiturns and milliturns. A turn is abbreviated τ or rev or rot depending on the application, but just r in rpm (revolutions per minute). 1 turn = 360° = 2π rad = 400 grad = 4 right angles.
- The quadrant is 1/4 of a turn, i.e. a right angle. It is the unit used in Euclid's Elements. 1 quad. = 90° = π/2 rad = 1/4 turn = 100 grad. In German the symbol ∟ has been used to denote a quadrant.
- The angle of the equilateral triangle is 1/6 of a turn. It was the unit used by the Babylonians[citation needed], and is especially easy to construct with ruler and compasses. The degree, minute of arc and second of arc are sexagesimal subunits of the Babylonian unit. 1 Babylonian unit = 60° = π/3 rad ≈ 1.047197551 rad.
- The radian is the angle subtended by an arc of a circle that has the same length as the circle's radius (k = 1 in the formula given earlier). One turn is 2π radians, and one radian is 180/π degrees, or about 57.2958 degrees. The radian is abbreviated rad, though this symbol is often omitted in mathematical texts, where radians are assumed unless specified otherwise. When radians are used angles are considered as dimensionless. The radian is used in virtually all mathematical work beyond simple practical geometry, due, for example, to the pleasing and "natural" properties that the trigonometric functions display when their arguments are in radians. The radian is the (derived) unit of angular measurement in the SI system.
- The astronomical hour angle is 1/24 of a turn. Since this system is amenable to measuring objects that cycle once per day (such as the relative position of stars), the sexagesimal subunits are called minute of time and second of time. Note that these are distinct from, and 15 times larger than, minutes and seconds of arc. 1 hour = 15° = π/12 rad = 1/6 quad. = 1/24 turn ≈ 16.667 grad.
- The point, used in navigation, is 1/32 of a turn. 1 point = 1/8 of a right angle = 11.25° = 12.5 grad. Each point is subdivided in four quarter-points so that 1 turn equals 128 quarter-points.
- Eratosthenes used a unit of 6° so that a whole turn was divided in 60 units.
- The Babylonians sometimes used the unit pechus of about 2° or 2½°.
- The binary degree, also known as the binary radian (or brad), is 1/256 of a turn.[4] The binary degree is used in computing so that an angle can be efficiently represented in a single byte (albeit to limited precision). Other measures of angle used in computing may be based on dividing one whole turn into 2n equal parts for other values of n.[5]
- The degree, denoted by a small superscript circle (°), is 1/360 of a turn, so one turn is 360°. One advantage of this old sexagesimal subunit is that many angles common in simple geometry are measured as a whole number of degrees. Fractions of a degree may be written in normal decimal notation (e.g. 3.5° for three and a half degrees), but the "minute" and "second" sexagesimal subunits of the "degree-minute-second" system are also in use, especially for geographical coordinates and in astronomy and ballistics:
- The diameter part (occasionally used in Islamic mathematics) is 1/60 radian. One "diameter part" is approximately 0.95493 degrees.
- The grad, also called grade, gradian, or gon, is 1/400 of a turn, so a right angle is 100 grads. It is a decimal subunit of the quadrant. A kilometre was historically defined as a centi-grad of arc along a great circle of the Earth, so the kilometer is the decimal analog to the sexagesimal nautical mile. The grad is used mostly in triangulation.
- The mil is approximately equal to a milliradian. There are several definitions ranging from 0.05625 to 0.06 degrees (3.375 to 3.6 minutes), with the milliradian being approximately 0.05729578 degrees (3.43775 minutes).
- The minute of arc (or MOA, arcminute, or just minute) is 1/60 of a degree = 1/3600 turn. It is denoted by a single prime ( ′ ). For example, 3° 30′ is equal to 3 + 30/60 degrees, or 3.5 degrees. A mixed format with decimal fractions is also sometimes used, e.g. 3° 5.72′ = 3 + 5.72/60 degrees. A nautical mile was historically defined as a minute of arc along a great circle of the Earth.
- The second of arc (or arcsecond, or just second) is 1/60 of a minute of arc and 1/3600 of a degree. It is denoted by a double prime ( ″ ). For example, 3° 7′ 30″ is equal to 3 + 7/60 + 30/3600 degrees, or 3.125 degrees.
Positive and negative angles
In mathematics, the angle from the first to the second coordinate axis of a coordinate system is considered as positive. Therefore angles given a sign are positive angles if measured anticlockwise, and negative angles if measured clockwise, from a given line. If no line is specified, it can be assumed to be the first coordinate axis (x-axis) in the Cartesian plane. In many geometrical situations a negative angle of −θ is effectively equivalent to a positive angle of "one full turn less θ". For example, a clockwise rotation of 45° (that is, an angle of −45°) is often effectively equivalent to an anticlockwise rotation of 360° − 45° (that is, an angle of 315°).
In three dimensional geometry, "clockwise" and "anticlockwise" have no absolute meaning, so the direction of positive and negative angles must be defined relative to some reference, which is typically a vector passing through the angle's vertex and perpendicular to the plane in which the rays of the angle lie.
In navigation, bearings are measured from north, increasing clockwise, so a bearing of 45 degrees is north-east. Negative bearings are not used in navigation, so north-west is 315 degrees.
Alternative ways of measuring the size of an angle
There are several alternatives to measuring the size of an angle by the corresponding angle of rotation. The grade of a slope, or gradient is equal to the tangent of the angle, or sometimes the sine. Gradients are often expressed as a percentage. For very small values (less than 5%), the grade of a slope is approximately the measure of an angle in radians.
In rational geometry the spread between two lines is defined at the square of sine of the angle between the lines. Since the sine of an angle and the sine of its supplementary angle are the same any angle of rotation that maps one of the lines into the other leads to the same value of the spread between the lines.
Astronomical approximations
Astronomers measure angular separation of objects in degrees from their point of observation.
- 1° is approximately the width of a little finger at arm's length.
- 10° is approximately the width of a closed fist at arm's length.
- 20° is approximately the width of a handspan at arm's length.
These measurements clearly depend on the individual subject, and the above should be treated as rough approximations only.
Identifying angles
In mathematical expressions, it is common to use Greek letters (α, β, γ, θ, φ, ...) to serve as variables standing for the size of some angle. (To avoid confusion with its other meaning, the symbol π is typically not used for this purpose.) Lower case roman letters (a, b, c, ...) are also used. See the figures in this article for examples.
In geometric figures, angles may also be identified by the labels attached to the three points that define them. For example, the angle at vertex A enclosed by the rays AB and AC (i.e. the lines from point A to point B and point A to point C) is denoted ∠BAC or BÂC. Sometimes, where there is no risk of confusion, the angle may be referred to simply by its vertex ("angle A").
Potentially, an angle denoted, say, ∠BAC might refer to any of four angles: the clockwise angle from B to C, the anticlockwise angle from B to C, the clockwise angle from C to B, or the anticlockwise angle from C to B, where the direction in which the angle is measured determines its sign (see Positive and negative angles). However, in many geometrical situations it is obvious from context that the positive angle less than or equal to 180 degrees is meant, and no ambiguity arises. Otherwise, a convention may be adopted so that ∠BAC always refers to the anticlockwise (positive) angle from B to C, and ∠CAB to the anticlockwise (positive) angle from C to B.
Types of angles
 The complementary angles a and b (b is the complement of a, and a is the complement of b).
The complementary angles a and b (b is the complement of a, and a is the complement of b).
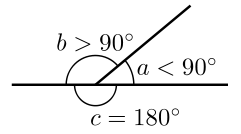 Acute (a), obtuse (b), and straight (c) angles. Here, a and b are supplementary angles.
Acute (a), obtuse (b), and straight (c) angles. Here, a and b are supplementary angles.
- An angle equal to 1/4 turn (90° or π/2 radians) is called a right angle.
- Two lines that form a right angle are said to be perpendicular or orthogonal.
- Angles equal to 1/2 turn (180° or two right angles) are called straight angles.
- Angles equal to 1 turn (360° or four right angles) are called full angles.
- Angles that are not right angles or a multiple of a right angle are called oblique angles.
- Angles smaller than a right angle (less than 90°) are called acute angles ("acute" meaning "sharp").
- Angles larger than a right angle and smaller than a straight angle (between 90° and 180°) are called obtuse angles ("obtuse" meaning "blunt").
- Angles larger than a straight angle but less than 1 turn (between 180° and 360°) are called reflex angles.
- Angles that have the same measure (i.e. the same magnitude) are said to be congruent. Following this definition for congruent angles, an angle is defined by its measure and is not dependent upon the lengths of the sides of the angle (e.g. all right angles are congruent).
- Two angles opposite each other, formed by two intersecting straight lines that form an "X"-like shape, are called vertical angles or opposite angles or vertically opposite angles. These angles are equal in measure.
- Angles that share a common vertex and edge but do not share any interior points are called adjacent angles.
- Two angles that sum to one right angle (90°) are called complementary angles.
- The difference between an angle and a right angle is termed the complement of the angle.
- Two angles that sum to a straight angle (180°) are called supplementary angles.
- The difference between an angle and a straight angle (180°) is termed the supplement of the angle.
- Two angles that sum to one turn (360°) are called explementary angles or conjugate angles.
- An angle that is part of a simple polygon is called an interior angle if it lies on the inside of that simple polygon. A concave simple polygon has at least one interior angle that exceeds 180°.
- In Euclidean geometry, the measures of the interior angles of a triangle add up to π radians, or 180°, or 1/2 turn; the measures of the interior angles of a simple quadrilateral add up to 2π radians, or 360°, or 1 turn. In general, the measures of the interior angles of a simple polygon with n sides add up to [(n − 2) × π] radians, or [(n − 2) × 180]°, or (2n − 4) right angles, or (n/2 − 1) turn.
- The angle supplementary to the interior angle is called the exterior angle. It measures the amount of rotation one has to make at this vertex to trace out the polygon. If the corresponding interior angle is a reflex angle, the exterior angle should be considered negative. Even in a non-simple polygon it may be possible to define the exterior angle, but one will have to pick an orientation of the plane (or surface) to decide the sign of the exterior angle measure.
- In Euclidean geometry, the sum of the exterior angles of a simple polygon will be one full turn (360°).
- Some authors use the name exterior angle of a simple polygon to simply mean the explementary (not supplementary!) of the interior angle.[6] This conflicts with the above usage.
- The angle between two planes (such as two adjacent faces of a polyhedron) is called a dihedral angle. It may be defined as the acute angle between two lines normal to the planes.
- The angle between a plane and an intersecting straight line is equal to ninety degrees minus the angle between the intersecting line and the line that goes through the point of intersection and is normal to the plane.
- Alternate angles, corresponding angle, interior angles and exterior angles are associated with a transversal of a pair of lines by a third.
- A reference angle is the acute version of any angle determined by repeatedly subtracting or adding 180 degrees, and subtracting the result from 180 degrees if necessary, until a value between 0 degrees and 90 degrees is obtained. For example, an angle of 30 degrees has a reference angle of 30 degrees, and an angle of 150 degrees also has a reference angle of 30 degrees (180-150). An angle of 750 degrees has a reference angle of 30 degrees (750-720).[7]
A formal definition
Using trigonometric functions
A Euclidean angle is completely determined by the corresponding right triangle. In particular, if θ is a Euclidean angle, then using trigonometric functions we find,
and
for two numbers x and y. So an angle in the Euclidean plane can be legitimately given by two numbers x and y.
To the ratio y/x there correspond two angles in the geometric range 0 < θ < 2π, since
If infinities are permitted for the quotient y/x one can define the angle θ as a function of x and y using the inverse tangent function for all points except the origin, assuming the inverse tangent varies from -π/2 to π/2,
The result will vary from -π to π. The values of x and y determine which quadrant the angle is in. Alternatively one can use the inverse cosine function assuming the result for the inverse cosine varies from 0 to π,
In this case the result will vary from 0 to 2π.
Angles between curves
The angle between a line and a curve (mixed angle) or between two intersecting curves (curvilinear angle) is defined to be the angle between the tangents at the point of intersection. Various names (now rarely, if ever, used) have been given to particular cases:—amphicyrtic (Gr. ἀμφί, on both sides, κυρτός, convex) or cissoidal (Gr. κισσός, ivy), biconvex; xystroidal or sistroidal (Gr. ξυστρίς, a tool for scraping), concavo-convex; amphicoelic (Gr. κοίλη, a hollow) or angulus lunularis, biconcave.[8]
Dot product and generalisation
In the Euclidean plane, the angle θ between two vectors u and v is related to their dot product and their lengths by the formula
This formula supplies an easy method to find the angle between two planes (or curved surfaces) from their normal vectors and between skew lines from their vector equations.
Inner product
To define angles in an abstract real inner product space, we replace the Euclidean dot product ( · ) by the inner product
 , i.e.
, i.e.In a complex inner product space, the expression for the cosine above may give non-real values, so it is replaced with
or, more commonly, using the absolute value, with
The latter definition ignores the direction of the vectors and thus describes the angle between one-dimensional subspaces
 and
and  spanned by the vectors
spanned by the vectors  and
and  correspondingly.
correspondingly.Angles between subspaces
The definition of the angle between one-dimensional subspaces
 and
and  given by
given byin a Hilbert space can be extended to subspaces of any finite dimensions. Given two subspaces
 with
with  , this leads to a definition of k angles called canonical or principal angles between subspaces.
, this leads to a definition of k angles called canonical or principal angles between subspaces.Angles in Riemannian geometry
In Riemannian geometry, the metric tensor is used to define the angle between two tangents. Where U and V are tangent vectors and gij are the components of the metric tensor G,
Angles in geography and astronomy
In geography, the location of any point on the Earth can be identified using a geographic coordinate system. This system specifies the latitude and longitude of any location in terms of angles subtended at the centre of the Earth, using the equator and (usually) the Greenwich meridian as references.
In astronomy, a given point on the celestial sphere (that is, the apparent position of an astronomical object) can be identified using any of several astronomical coordinate systems, where the references vary according to the particular system. Astronomers measure the angular separation of two stars by imagining two lines through the centre of the Earth, each intersecting one of the stars. The angle between those lines can be measured, and is the angular separation between the two stars.
Astronomers also measure the apparent size of objects as an angular diameter. For example, the full moon has an angular diameter of approximately 0.5°, when viewed from Earth. One could say, "The Moon's diameter subtends an angle of half a degree." The small-angle formula can be used to convert such an angular measurement into a distance/size ratio.
See also
- Angle bisector
- Argument (complex analysis)
- Astrological aspect
- Central angle
- Clock angle problem
- Complementary angles
- Great circle distance
- Inscribed angle
- Protractor
- Solid angle for a concept of angle in three dimensions.
- Supplementary angles
- Irrational angle
- Angular velocity
Notes
- ^ Sidorov, L.A. (2001), "Angle", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/A/a012500.htm
- ^ Slocum, Jonathan (2007), Preliminary Indo-European lexicon — Pokorny PIE data, University of Texas research department: linguistics research center, http://www.utexas.edu/cola/centers/lrc/ielex/X/P0089.html, retrieved 2 Feb., 2010
- ^ Chisholm 1911; Heiberg 1908, pp. 177–178
- ^ ooPIC Programmer's Guide (archived) www.oopic.com
- ^ Angles, integers, and modulo arithmetic Shawn Hargreaves blogs.msdn.com
- ^ Weisstein, Eric W., "Exterior Angle" from MathWorld.
- ^ http://www.mathwords.com/r/reference_angle.htm
- ^ Chisholm 1911; Heiberg 1908, p. 178
References
- Heiberg, Johan Ludvig (1908). Heath, T. L.. ed. Euclid. The thirteen books of Euclid's Elements. 1. http://books.google.com/books?id=UhgPAAAAIAAJ.
- Attribution
 This article incorporates text from a publication now in the public domain: Chisholm, Hugh, ed (1911). "Angle". Encyclopædia Britannica (11th ed.). Cambridge University Press.
This article incorporates text from a publication now in the public domain: Chisholm, Hugh, ed (1911). "Angle". Encyclopædia Britannica (11th ed.). Cambridge University Press.
External links
- Angle Bisectors in a Quadrilateral at cut-the-knot
- Constructing a triangle from its angle bisectors at cut-the-knot
- Angle Estimation – for basic astronomy.
- Angle definition pages with interactive applets.
- Various angle constructions with compass and straightedge
- GonioLab DD – Convert between DecDeg and DegMinSec and vice-versa (requires Java Web Start)
Categories:- Elementary geometry
- Trigonometry
- Angle
Wikimedia Foundation. 2010.












![\theta(x,y)=\begin{cases}cos^{-1}[x/r(x,y)]&y\ge 0\\2\pi-cos^{-1}[x/r(x,y)]&y<0\end{cases}](4/664a8740969c7730f1ac30a4d3308e7f.png)






