- Logical conjunction
-
"∧" redirects here. For exterior product, see exterior algebra.
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false.
The analogue of conjunction for a (possibly infinite) family of statements is universal quantification, which is part of predicate logic.
Contents
Notation
And is usually expressed with the prefix operator K, or an infix operator. In mathematics and logic, the infix operator is usually ∧; in electronics
 ; and in programming languages, & or and. Some programming languages have a related control structure, the short-circuit and, written &&, and then, etc.
; and in programming languages, & or and. Some programming languages have a related control structure, the short-circuit and, written &&, and then, etc.Definition
Logical conjunction is an operation on two logical values, typically the values of two propositions, that produces a value of true if and only if both of its operands are true.
Truth table
The truth table of
 :
:INPUT OUTPUT A B A AND B 0 0 0 0 1 0 1 0 0 1 1 1 Introduction and elimination rules
As a rule of inference, conjunction introduction is a classically valid, simple argument form. The argument form has two premises, A and B. Intuitively, it permits the inference of their conjunction.
- A,
- B.
- Therefore, A and B.
or in logical operator notation:
- A,
- B

Here is an example of an argument that fits the form conjunction introduction:
- Bob likes apples.
- Bob likes oranges.
- Therefore, Bob likes apples and oranges.
Conjunction elimination is another classically valid, simple argument form. Intuitively, it permits the inference from any conjunction of either element of that conjunction.
- A and B.
- Therefore, A.
...or alternately,
- A and B.
- Therefore, B.
In logical operator notation:
...or alternately,
Properties
commutativity: yes






associativity: yes








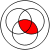

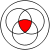

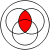

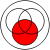
distributivity: with various operations, especially with or









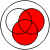





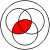
others with exclusive or:











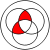




with material nonimplication:









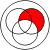

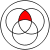




with itself:
















idempotency: yes










monotonicity: yes












truth-preserving: yes
When all inputs are true, the output is true.





(to be tested) falsehood-preserving: yes
When all inputs are false, the output is false.





(to be tested) Walsh spectrum: (1,-1,-1,1)
Nonlinearity: 1 (the function is bent)
If using binary values for true (1) and false (0), then logical conjunction works exactly like normal arithmetic multiplication.
Applications in computer engineering
 AND logic gate
AND logic gate
In high-level computer programming and digital electronics, logical conjunction is commonly represented by an infix operator, usually as a keyword such as "
AND", an algebraic multiplication, or the ampersand symbol "&". Many languages also provide short-circuit control structures corresponding to logical conjunction.Logical conjunction is often used for bitwise operations, where
0corresponds to false and1to true:0 AND 0=0,0 AND 1=0,1 AND 0=0,1 AND 1=1.
The operation can also be applied to two binary words viewed as bitstrings of equal length, by taking the bitwise AND of each pair of bits at corresponding positions. For example:
11000110 AND 10100011=10000010.
This can be used to select part of a bitstring using a bit mask. For example,
10011101 AND 00001000=00001000extracts the fifth bit of an 8-bit bitstring.In computer networking, bit masks are used to derive the network address of a subnet within an existing network from a given IP address, by ANDing the IP address and the subnet mask.
Logical conjunction "
AND" is also used in SQL operations to form database queries.The Curry-Howard correspondence relates logical conjunction to product types.
Set-theoretic intersection
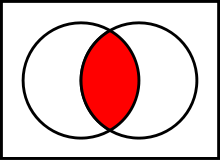
The intersection used in set theory is defined in terms of a logical conjunction: x ∈ A ∩ B if and only if (x ∈ A) ∧ (x ∈ B). Because of this, set-theoretic intersection shares several properties with logical conjunction, such as associativity, commutativity, and idempotence.
Natural language
The logical conjunction and in logic is related to, but not the same as, the grammatical conjunction and in natural languages.
English "and" has properties not captured by logical conjunction. For example, "and" sometimes implies order. For example, "They got married and had a child" in common discourse means that the marriage came before the child. The word "and" can also imply a partition of a thing into parts, as "The American flag is red, white, and blue." Here it is not meant that the flag is at once red, white, and blue, but rather that it has a part of each color.
See also
- And-inverter graph
- AND gate
- Binary and
- Bitwise AND
- Boolean algebra (logic)
- Boolean algebra topics
- Boolean conjunctive query
- Boolean domain
- Boolean function
- Boolean-valued function
- Conjunction introduction
- Conjunction elimination
- De Morgan's laws
- First-order logic
- Grammatical conjunction
- Logical disjunction
- Logical negation
- Logical graph
- Logical value
- Operation
- Peano-Russell notation
- Propositional calculus
External links
Logical connectives  Categories:
Categories:- Logical connectives
- Boolean algebra
- Binary operations
- Propositional calculus
Wikimedia Foundation. 2010.