- Net (polyhedron)
-
 Net of a dodecahedron
Net of a dodecahedron
 When the Earth is mapped on a polyhedron, its net is a flat world map, e.g. the Dymaxion map using the regular icosahedron and a few subdivisions of the triakis icosahedron.
When the Earth is mapped on a polyhedron, its net is a flat world map, e.g. the Dymaxion map using the regular icosahedron and a few subdivisions of the triakis icosahedron.
In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded (along edges) to become the faces of the polyhedron. Polyhedral nets are a useful aid to the study of polyhedra and solid geometry in general, as they allow for models of polyhedra to be constructed from material such as thin cardboard.
It is a long-standing open question whether or not every convex polyhedron P (one without "dents" – in other words, all dihedral angles between the edges are ≤ 180 degrees) has a net: whether the surface P may be cut along edges and unfolded flat to a planar polygon (without overlap). (This system of edges is sometimes denoted as the polyhedron's unfolding.) The problem was first explicitly posed in a paper by Shephard.[1] The history of and progress on this question is discussed in Part III of Geometric Folding Algorithms.[2] If the restriction that the cuts be along polyhedron edges is relaxed to permit cuts through the interior of faces, then there are several known methods to cut and unfold a convex polyhedron to a planar polygon. For example, cutting along the cut locus of a point suffices.
Also, the shortest path over the surface between two points on the surface of a polyhedron corresponds to a straight line on a suitable net. The net has to be such that the straight line is fully within it, and one may have to consider several nets to see which gives the shortest path. For example, in the case of a cube, if the points are on adjacent faces one candidate for the shortest path is the path crossing the common edge; the shortest path of this kind is found using a net where the two faces are also adjacent. Other candidates for the shortest path are through the surface of a third face adjacent to both (of which there are two), and corresponding nets can be used to find the shortest path in each category.
Contents
Higher dimensional polytope nets
The geometric concept of a net can be extended to higher dimensions.

Tesseract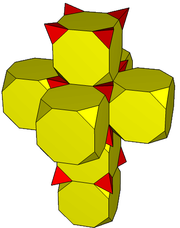
Truncated tesseract
24-cellFor example, a net of a polychoron, or four-dimensional polytope, is composed of polyhedral cells that are connected by their faces and all occupy the same three-dimensional space, just as the polygon faces of a net of a polyhedron are connected by their edges and all occupy the same plane. The tesseract, the four-dimensional cube, is used prominently in a 1954 painting by Salvador Dali, Crucifixion (Corpus Hypercubus).
Whether or not every four-dimensional polytope may be cut along the two-dimensional faces shared by its three-dimensional facets, and unfolded into 3D to a single nonoverlapping polyhedron (as in the above unfolding of the tesseract), remains unknown, as does the corresponding question in higher dimensions.
See also
- Paper model
- Cardboard modeling
- UV mapping
References
- ^ Shephard, Geoffrey (1975), "Convex Polytopes with Convex Nets", Math. Proc. Camb. Phil. Soc. 78 (3): 389–403, doi:10.1017/S0305004100051860, ISSN 1469-8064
- ^ Demaine, Erik; O'Rourke, Joseph (July 2007), Geometric Folding Algorithms: Linkages, Origami, Polyhedra, Cambridge University Press, ISBN 978-0-521-85757-4, http://www.gfalop.org
External links
- Weisstein, Eric W., "Net" from MathWorld.
- Weisstein, Eric W., "Unfolding" from MathWorld.
- Weisstein, Eric W., "Shephard's Conjecture" from MathWorld.
- Nets: A Tool for Representing Polyhedra in Two Dimensions
- Nuts About Nets!, George Olshevsky.
- Regular 4d Polytope Foldouts
- Editable Printable Polyhedral Nets with an Interactive 3D View
- Paper Models of Polyhedra
- Unfolder for Blender
- Unfolding package for Mathematica
Categories:- Polygons
- Polyhedra
- Polychora
- Polytopes
Wikimedia Foundation. 2010.
