- Dispersion (water waves)
-
This article is about dispersion of waves on a water surface. For other forms of dispersion, see Dispersion (disambiguation).
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension. As a result, water with a free surface is generally considered to be a dispersive medium.
Surface gravity waves, moving under the forcing by gravity, propagate faster for increasing wavelength. For a given wavelength, gravity waves in deeper water have a larger phase speed than in shallower water. In contrast with this, capillary waves only forced by surface tension, propagate faster for shorter wavelengths.
Besides frequency dispersion, water waves also exhibit amplitude dispersion. This is a nonlinear effect, by which waves of larger amplitude have a different phase speed from small-amplitude waves.
Contents
Frequency dispersion for surface gravity waves
This section is about frequency dispersion for waves on a fluid layer forced by gravity, and according to linear theory.
Wave propagation and dispersion
The simplest propagating wave of unchanging form is a sine wave. A sine wave with water surface elevation η( x, t ) is given by:[1]
where a is the amplitude (in metres) and θ = θ( x, t ) is the phase function (in radians), depending on the horizontal position ( x , in metres) and time ( t , in seconds):[2]
 with
with  and
and 
where:
- λ is the wavelength (in metres),
- T is the period (in seconds),
- k is the wavenumber (in radians per metre) and
- ω is the angular frequency (in radians per second).
Characteristic phases of a water wave are:
- the upward zero-crossing at θ = 0,
- the wave crest at θ = ½ π,
- the downward zero-crossing at θ = π and
- the wave trough at θ = 1½ π.
A certain phase repeats itself after an integer m multiple of 2π: sin(θ) = sin(θ+m•2π).
Essential for water waves, and other wave phenomena in physics, is that free propagating waves of non-zero amplitude only exist when the angular frequency ω and wavenumber k (or equivalently the wavelength λ and period T ) satisfy a functional relationship: the frequency dispersion relation[3][4]
The dispersion relation has two solutions: ω = +Ω(k) and ω = -Ω(k), corresponding to waves travelling in the positive or negative x–direction. The dispersion relation will in general depend on several other parameters in addition to the wavenumber k. For gravity waves, according to linear theory, these are the acceleration by gravity and the water depth.
An initial wave phase θ = θ0 propagates as a function of space and time. Its subsequent position is given by:
This shows that the phase moves with the velocity:[1]
which is called the phase velocity.
Phase velocity
Further information: Phase velocityA sinusoidal wave, of small surface-elevation amplitude and with a constant wavelength, propagates with the phase velocity, also called celerity or phase speed. While the phase velocity is a vector and has an associated direction, celerity or phase speed refer only to the magnitude of the phase velocity. According to linear theory for waves forced by gravity, the phase speed depends on the wavelength and the water depth. For a fixed water depth, long waves (with large wavelength) propagate faster than shorter waves.
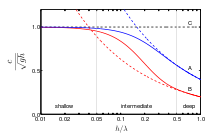
In the left figure, it can be seen that shallow water waves, with wavelengths λ much larger than the water depth h, travel with the phase velocity[1]
with g the acceleration by gravity and cp the phase speed. Since this shallow-water phase speed is independent of the wavelength, shallow water waves do not have frequency dispersion.
Using another normalization for the same frequency dispersion relation, the figure on the right shows that in deep water, with water depth h larger than half the wavelength λ (so for h/λ > 0.5), the phase velocity cp is independent of the water depth:[1]
with T the wave period (the reciprocal of the frequency f, T=1/f ). So in deep water the phase speed increases with the wavelength, and with the period.
Since the phase speed satisfies cp = λ/T = λf, wavelength and period (or frequency) are related. For instance in deep water:
The dispersion characteristics for intermediate depth are given below.
Group velocity
Further information: Group velocity Frequency dispersion in bichromatic groups of gravity waves on the surface of deep water. The red dot moves with the phase velocity, and the green dots propagate with the group velocity.
Frequency dispersion in bichromatic groups of gravity waves on the surface of deep water. The red dot moves with the phase velocity, and the green dots propagate with the group velocity.
More … In this deep-water case, the phase velocity is twice the group velocity. The red dot overtakes two green dots, when moving from the left to the right of the figure.
New waves seem to emerge at the back of a wave group, grow in amplitude until they are at the center of the group, and vanish at the wave group front.
For gravity surface-waves, the water particle velocities are much smaller than the phase velocity, in most cases.Interference of two sinusoidal waves with slightly different wavelengths, but the same amplitude and propagation direction, results in a beat pattern, called a wave group. As can be seen in the animation, the group moves with a group velocity cg different from the phase velocity cp, due to frequency dispersion.
The group velocity is depicted by the red lines (marked B) in the two figures above. In shallow water, the group velocity is equal to the shallow-water phase velocity. This is because shallow water waves are not dispersive. In deep water, the group velocity is equal to half the phase velocity: cg = ½ cp.[5]
The group velocity also turns out to be the energy transport velocity. This is the velocity with which the mean wave energy is transported horizontally in a narrow-band wave field.[6][7]
In case of a the group velocity different from the phase velocity, a consequence is that the number of waves counted in a wave group is different when counted from a snapshot in space at a certain moment, from when counted in time from the measured surface elevation at a fixed position. Consider a wave group of length Λg and group duration of τg. The group velocity is:[8]
 The number of waves per group as observed in space at a certain moment (upper blue line), is different from the number of waves per group seen in time at a fixed position (lower orange line), due to frequency dispersion.
The number of waves per group as observed in space at a certain moment (upper blue line), is different from the number of waves per group seen in time at a fixed position (lower orange line), due to frequency dispersion.
More … For the shown case, a bichromatic group of gravity waves on the surface of deep water, the group velocity is half the phase velocity. In this example, there are 5.75 waves between two wave group nodes in space, while there are 11.5 waves between two wave group nodes in time.  North Pacific storm waves as seen from the NOAA M/V Noble Star, Winter 1989.
North Pacific storm waves as seen from the NOAA M/V Noble Star, Winter 1989.
The number of waves in a wave group, measured in space at a certain moment is: Λg / λ. While measured at a fixed location in time, the number of waves in a group is: τg / T. So the ratio of the number of waves measured in space to those measured in time is:
So in deep water, with cg = ½ cp,[9] a wave group has twice as many waves in time as it has in space.
The water surface elevation η(x,t), as a function of horizontal position x and time t, for a bichromatic wave group of full modulation can be mathematically formulated as:[9]
with:
- a the wave amplitude of each frequency component in metres,
- k1 and k2 the wave number of each wave component, in radians per metre, and
- ω1 and ω2 the angular frequency of each wave component, in radians per second.
Both ω1 and k1, as well as ω2 and k2, have to satisfy the dispersion relation:
 and
and 
Using trigonometric identities, the surface elevation is written as:[8]
The part between square brackets is the slowly-varying amplitude of the group, with group wave number ½ ( k1 - k2 ) and group angular frequency ½ ( ω1 - ω2 ). As a result, the group velocity is, for the limit k1 → k2 :[8][9]
Wave groups can only be discerned in case of a narrow-banded signal, with the wave-number difference k1 - k2 small compared to the mean wave number ½ (k1 + k2).
Multi-component wave patterns
 Frequency dispersion of surface gravity waves on deep water. The superposition (dark blue line) of three sinusoidal wave components (light blue lines) is shown.
Frequency dispersion of surface gravity waves on deep water. The superposition (dark blue line) of three sinusoidal wave components (light blue lines) is shown.More … For the three components respectively 22 (bottom), 25 (middle) and 29 (top) wavelengths fit in a horizontal domain of 2,000 meter length. The component with the shortest wavelength (top) propagates slowest. The wave amplitudes of the components are respectively 1, 2 and 1 meter. The differences in wavelength and phase speed of the components results in a changing pattern of wave groups, due to amplification where the components are in phase, and reduction where they are in anti-phase. The effect of frequency dispersion is that the waves travel as a function of wavelength, so that spatial and temporal phase properties of the propagating wave are constantly changing. For example, under the action of gravity, water waves with a longer wavelength travel faster than those with a shorter wavelength.
While two superimposed sinusoidal waves, called a bichromatic wave, have an envelope which travels unchanged, three or more sinusoidal wave components result in a changing pattern of the waves and their envelope. A sea state – that is: real waves on the sea or ocean – can be described as a superposition of many sinusoidal waves with different wavelengths, amplitudes, initial phases and propagation directions. Each of these components travels with its own phase velocity, in accordance with the dispersion relation. The statistics of such a surface can be described by its power spectrum.[10]
Dispersion relation
In the table below, the dispersion relation ω2 = [Ω(k)]2 between angular frequency ω = 2π / T and wave number k = 2π / λ is given, as well as the phase and group speeds.[8]
Frequency dispersion of gravity waves on the surface of deep water, shallow water and at intermediate depth, according to linear wave theory quantity symbol units deep water
( h > ½ λ )shallow water
( h < 0.05 λ )intermediate depth
( all λ and h )dispersion relation 
rad / s 

![\begin{align}
&\sqrt{ gk\, \tanh\left( kh \right)}\,
\\[1.2ex]
&=\sqrt{\frac{2\pi g}{\lambda}\tanh\left(\frac{2\pi h}{\lambda}\right)}\,
\end{align}](6/e56ad12d265a05dd56c46daeb7e929ea.png)
phase velocity 
m / s 


group velocity 
m / s 


ratio 
- 


wavelength 
m 

for given period T, the solution of:

Deep water corresponds with water depths larger than half the wavelength, which is the common situation in the ocean. In deep water, longer period waves propagate faster and transport their energy faster. The deep-water group velocity is half the phase velocity. In shallow water, for wavelengths larger than twenty times the water depth,[11] as found quite often near the coast, the group velocity is equal to the phase velocity.
History
The full linear dispersion relation was first found by Pierre-Simon Laplace, although there were some errors in his solution for the linear wave problem. The complete theory for linear water waves, including dispersion, was derived by George Biddell Airy and published in about 1840. A similar equation was also found by Philip Kelland at around the same time (but making some mistakes in his derivation of the wave theory).[12]
The shallow water (with small h / λ) limit, ω2 = gh k2, was derived by Joseph Louis Lagrange.
Surface tension effects
Further information: Capillary wave Dispersion of gravity-capillary waves on the surface of deep water. Phase and group velocity divided by
Dispersion of gravity-capillary waves on the surface of deep water. Phase and group velocity divided by
![\scriptstyle \sqrt[4]{g\sigma/\rho}](0/f105d8e7515021ac7d03beb9f12fb7d5.png) as a function of relative wavelength
as a function of relative wavelength  .
.
Blue lines (A): phase velocity, Red lines (B): group velocity.
Drawn lines: dispersion relation for gravity-capillary waves.
Dashed lines: dispersion relation for deep-water gravity waves.
Dash-dot lines: dispersion relation valid for deep-water capillary waves.In case of gravity-capillary waves, where surface tension affects the waves, the dispersion relation becomes:[4]
with σ the surface tension (in N/m).
Nonlinear effects
Shallow water
Amplitude dispersion effects appear for instance in the solitary wave (or soliton): a single hump of water traveling with constant velocity in shallow water with a horizontal bed. The single soliton solution of the Korteweg–de Vries equation, of wave height H in water depth h far away from the wave crest, travels with the velocity:
So for this nonlinear gravity wave it is the total water depth under the wave crest that determines the speed, with higher waves traveling faster than lower waves. Note that soliton solutions only exist for positive values of H, solitary gravity waves of depression do not exist.
Deep water
The linear dispersion relation – unaffected by wave amplitude – is for nonlinear waves also correct at the second order of the perturbation theory expansion, with the orders in terms of the wave steepness k A (where A is wave amplitude). To the third order, and for deep water, the dispersion relation is[13]
This implies that large waves travel faster than small ones of the same frequency. This is only noticeable when the wave steepness k A is large.
Waves on a mean current: Doppler shift
Water waves on a mean flow (so a wave in a moving medium) experience a Doppler shift. Suppose the dispersion relation for a non-moving medium is:
with k the wavenumber. Then for a medium with mean velocity vector V, the dispersion relationship with Doppler shift becomes:[14]
where k is the wavenumber vector, related to k as: k = |k|. The inner product k•V is equal to: k•V = kV cos α, with V the length of the mean velocity vector V: V = |V|. And α the angle between the wave propagation direction and the mean flow direction. For waves and current in the same direction, k•V=kV.
See also
Other articles on dispersion
Dispersive water-wave models
- Airy wave theory
- Benjamin–Bona–Mahony equation
- Boussinesq approximation (water waves)
- Camassa-Holm equation
- Davey–Stewartson equations
- Kadomtsev–Petviashvili equation or KP equation
- Korteweg–de Vries equation (or KdV equation)
- Luke's variational principle
- Nonlinear Schrödinger equation
- Shallow water equations
Notes
- ^ a b c d See Lamb (1994), §229, pp. 366–369.
- ^ See Whitham (1974), p.11.
- ^ This dispersion relation is for a non-moving homogeneous medium, so in case of water waves for a constant water depth and no mean current.
- ^ a b See Phillips (1977), p. 37.
- ^ See Phillips (1977), p. 25.
- ^ Reynolds, O. (1877), "On the rate of progression of groups of waves and the rate at which energy is transmitted by waves", Nature 16: 343–44
Lord Rayleigh (J. W. Strutt) (1877), "On progressive waves", Proceedings of the London Mathematical Society 9: 21–26, doi:10.1112/plms/s1-9.1.21 Reprinted as Appendix in: Theory of Sound 1, MacMillan, 2nd revised edition, 1894. - ^ See Lamb (1994), §237, pp. 382–384.
- ^ a b c d See Dingemans (1997), section 2.1.2, pp. 46–50.
- ^ a b c See Lamb (1994), §236, pp. 380–382.
- ^ See Phillips (1977), p. 102.
- ^ See Dean and Dalrymple (1991), page 65.
- ^ See Craik (2004).
- ^ See Lamb (1994), §250, pp. 417–420.
- ^ See Phillips (1977), p. 24.
References
- Craik, A.D.D. (2004), "The origins of water wave theory", Annual Review of Fluid Mechanics 36: 1–28, Bibcode 2004AnRFM..36....1C, doi:10.1146/annurev.fluid.36.050802.122118
- Dean, R.G.; Dalrymple, R.A. (1991), Water wave mechanics for engineers and scientists, Advanced Series on Ocean Engineering, 2, World Scientific, Singapore, ISBN 978 981 02 0420 4, OCLC 22907242
- Dingemans, M.W. (1997), Water wave propagation over uneven bottoms, Advanced Series on Ocean Engineering, 13, World Scientific, Singapore, ISBN 981 02 0427 2, OCLC 36126836, 2 Parts, 967 pages.
- Lamb, H. (1994), Hydrodynamics (6th ed.), Cambridge University Press, ISBN 978 0 521 45868 9, OCLC 30070401 Originally published in 1879, the 6th extended edition appeared first in 1932.
- Landau, L.D.; Lifshitz, E.M. (1987), Fluid Mechanics, Course of theoretical physics, 6 (2nd ed.), Pergamon Press, ISBN 0 08 339932 8
- Lighthill, M.J. (1978), Waves in fluids, Cambridge University Press, ISBN 0 521 29233 6, OCLC 2966533
- Phillips, O.M. (1977), The dynamics of the upper ocean (2nd ed.), Cambridge University Press, ISBN 0 521 29801 6, OCLC 7319931
- Whitham, G. B. (1974), Linear and nonlinear waves, Wiley-Interscience, ISBN 0 471 94090 9, OCLC 815118
External links
- Mathematical aspects of dispersive waves are discussed on the Dispersive Wiki.
Categories:- Water waves
- Wave mechanics
- Fluid dynamics
- Physical oceanography
Wikimedia Foundation. 2010.













![\eta= \left[ 2\, a\, \cos \left( \frac{k_1 - k_2}{2} x - \frac{\omega_1 - \omega_2}{2} t \right) \right]\;
\cdot\;
\sin \left( \frac{k_1 + k_2}{2} x - \frac{\omega_1 + \omega_2}{2} t \right).](f/fef808e433f884ade248ba8f504852cb.png)



![\omega^2 = gk \left[1+(kA)^2\right].](e/2aeb4e732197fa1f29ddfd8d49936f35.png)