- Magic hexagon
-
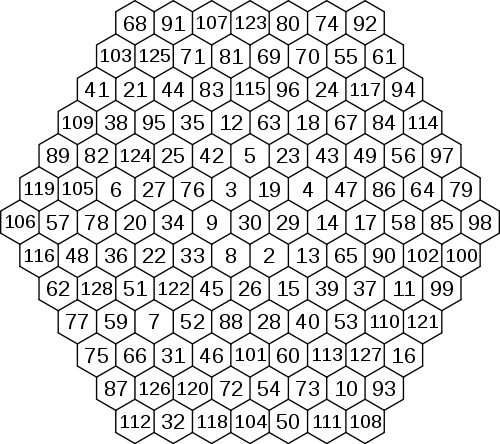
A magic hexagon of order n is an arrangement of numbers in a centered hexagonal pattern with n cells on each edge, in such a way that the numbers in each row, in all three directions, sum to the same magic constant. A normal magic hexagon contains the consecutive integers from 1 to 3n2 − 3n + 1. It turns out that magic hexagons exist only for n = 1 (which is trivial) and n = 3. Moreover, the solution of order 3 is essentially unique.[1] Meng also gave a less intricate constructive proof.[2]

Order 1
M = 1Order n=3
M = 38The order-3 magic hexagon has been published many times as a 'new' discovery. An early reference, and possibly the first discoverer, is Ernst von Haselberg (1887).
Although there are no normal magical hexagons with order greater than 3, certain abnormal ones do exist. In this case, abnormal means starting the sequence of numbers other than with 1. Arsen Zahray discovered these order 4 and 5 hexagons:
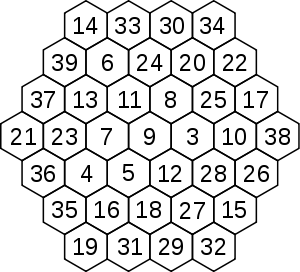
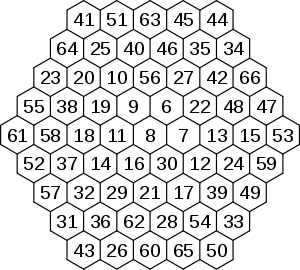
Order 4
M = 111Order 5
M = 244The order 4 hexagon starts with 3 and ends with 39, its rows summing to 111. The order 5 hexagon starts with 6 and ends with 66 and sums to 244.
An order 6 hexagon can be seen below. It was created by Louis Hoelbling, October 11, 2004:
It starts with 21, ends with 111, and its sum is 546.
The largest magic hexagon so far was discovered using simulated annealing by Arsen Zahray on 22 March 2006:
It starts with 2, ends with 128 and its sum is 635.
However, a slightly larger, order 8 magic hexagon was generated by Louis K. Hoelbling on February 5, 2006:

It starts with -84 and ends with 84, and its sum is 0.
Contents
Proof
Here is a proof sketch that no normal magic hexagons exist except those of order 1 and 3.
The magic constant M of a normal magic hexagon can be determined as follows. The numbers in the hexagon are consecutive, and run from 1 to (3n^2-3n+1). Hence their sum is a triangular number, namely
There are r = (2n − 1) rows running along any given direction (E-W, NE-SW, or NW-SE). Each of these rows sum up to the same number M. Therefore:
Rewriting this as
shows that 5/(2n − 1) must be an integer. The only n ≥ 1 that meet this condition are n = 1 and n = 3.
Another type of magic hexagon
Hexagons can also be constructed with triangles, as the following diagrams show.


Order 2 Order 2 with numbers 1–24 This type of configuration can be called a T-hexagon and it has many more properties than the hexagon of hexagons.
As with the above, the rows of triangles run in three directions and there are 24 triangles in a T-hexagon of order 2. In general, a T-hexagon of order n has 6n2 triangles. The sum of all these numbers is given by:
If we try to construct a magic T-hexagon of side n, we have to choose n to be even, because there are r = 2n rows so the sum in each row must be
For this to be an integer, n has to be even. To date, magic T-hexagons of order 2, 4, 6 and 8 have been discovered. The first was a magic T-hexagon of order 2, discovered by John Baker on 13 September 2003. Since that time, John has been collaborating with David King, who discovered that there are 59,674,527 non-congruent magic T-hexagons of order 2.
Magic T-hexagons have a number of properties in common with magic squares, but they also have their own special features. The most surprising of these is that the sum of the numbers in the triangles that point upwards is the same as the sum of those in triangles that point downwards (no matter how large the T-hexagon). In the above example,
- 17 + 20 + 22 + 21 + 2 + 6 + 10 + 14 + 3 + 16 + 12 + 7
- = 5 + 11 + 19 + 9 + 8 + 13 + 4 + 1 + 24 + 15 + 23 + 18
- = 150
To find out more about magic T-hexagons, visit Hexagonia or the Hall of Hexagons.
Notes
- ^ <Trigg, C. W. "A Unique Magic Hexagon", Recreational Mathematics Magazine, January–February 1964. Retrieved on 2009-12-16.
- ^ <Meng, F. "Research into the Order 3 Magic Hexagon", Shing-Tung Yau Awards, October 2008. Retrieved on 2009-12-16.
References
- Baker. J. E. and King, D. R. (2004) "The use of visual schema to find properties of a hexagon" Visual Mathematics, Volume 5, Number 3
- Baker, J. E. and Baker, A. J. (2004) "The hexagon, nature's choice" Archimedes, Volume 4
See also
- hexagonal tortoise problem
Categories:- Magic squares
Wikimedia Foundation. 2010.