- Disdyakis triacontahedron
-
Disdyakis triacontahedron 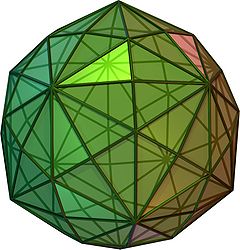
Click on picture for large version
spinning version
Type Catalan Face polygon scalene triangle Faces 120 Edges 180 Vertices 62 = 12 + 20 + 30 Face configuration V4.6.10 Symmetry group Ih, [5,3], *532 Dihedral angle 164° 53' 17" Dual polyhedron truncated icosidodecahedron Properties convex, face-transitive 
NetIn geometry, a disdyakis triacontahedron, or hexakis icosahedron is a Catalan solid and the dual to the Archimedean truncated icosidodecahedron. As such it is face uniform but with irregular face polygons. It looks a bit like an inflated rhombic triacontahedron—if one replaces each face of the rhombic triacontahedron with a single vertex and four triangles in a regular fashion one ends up with a disdyakis triacontahedron. That is, the disdyakis triacontahedron is the Kleetope of the rhombic triacontahedron. It also has the most faces among the Archimedean and Catalan solids, with in second place the Snub dodecahedron, which is an enneacontadihedron.
The edges of the polyhedron projected onto a sphere form great circles, and represent all ten mirror planes of reflective Ih icosahedral symmetry, as shown in this image. Combining pairs of light and dark triangles define the fundamental domains of the nonreflective I icosahedral symmetry.


See also
- Tetrakis cube, an icositetrahedral relative
- Disdyakis dodecahedron, a tetracontaoctahedral relative
- Bisected hexagonal tiling
References
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR730208 (The thirteen semiregular convex polyhedra and their duals, Page 25, Disdyakistriacontahedron )
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 285, kisRhombic triacontahedron )
External links
- Eric W. Weisstein, Disdyakis triacontahedron (Catalan solid) at MathWorld.
- Disdyakis triacontahedron (Hexakis Icosahedron) -- Interactive Polyhedron Model
Polyhedron navigator Platonic solids (regular) Archimedean solids
(Semiregular/Uniform)Catalan solids
(Dual semiregular)triakis tetrahedron · rhombic dodecahedron · triakis octahedron · tetrakis cube · deltoidal icositetrahedron · disdyakis dodecahedron · pentagonal icositetrahedron · rhombic triacontahedron · triakis icosahedron · pentakis dodecahedron · deltoidal hexecontahedron · disdyakis triacontahedron · pentagonal hexecontahedronDihedral regular Dihedral uniform Duals of dihedral uniform Dihedral others Degenerate polyhedra are in italics. 
This polyhedron-related article is a stub. You can help Wikipedia by expanding it.
