- Dihedron
-
Set of regular n-gonal dihedrons 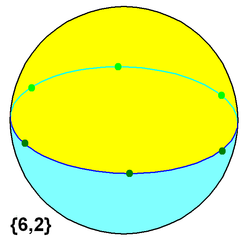
Example hexagonal dihedron on a sphereType Regular polyhedron
or spherical tilingFaces 2 n-gons Edges n Vertices n Schläfli symbol {n,2} Vertex configuration n2 Coxeter–Dynkin diagram 




Wythoff symbol 2 | n 2 Symmetry group Dnh, [2,n], (*22n) Dual polyhedron hosohedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is the fundamental domain of a lens space L(p,q).[1]
Usually a regular dihedron is implied (two regular polygons) and this gives it a Schläfli symbol as {n, 2}.
The dual of a n-gonal dihedron is the n-gonal hosohedron, where n digon faces share two vertices.
Contents
As a polyhedron
A dihedron can be considered a degenerate prism consisting of two (planar) n-sided polygons connected "back-to-back", so that the resulting object has no depth.
From a Wythoff construction on dihedral symmetry, a truncation operation on a regular {n,2} dihedron transforms it into a 4.4.n n-prism.
As a tiling on a sphere
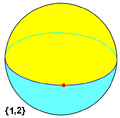
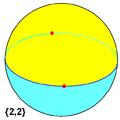
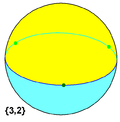
As a spherical tiling, a dihedron can exist as nondegenerate form, with two n-sided faces covering the sphere, each face being a hemisphere, and vertices around a great circle. (It is regular if the vertices are equally spaced.)
The regular polyhedron {2,2} is self-dual, and is both a hosohedron and a dihedron.
Regular dihedron examples: (spherical tilings)

Ditopes
A regular ditope is an n-dimensional analogue of a dihedron, with Schläfli symbol {p,..q,r,2}. It has two facets, {p,...,q,r}, which share all ridges, {p,...,q} in common.
See also
Notes
- ^ Gausmann, Evelise; Roland Lehoucq, Jean-Pierre Luminet, Jean-Philippe Uzan, Jeffrey Weeks (2001). "Topological Lensing in Spherical Spaces". Classical and Quantum Gravity 18: 5155–5186. arXiv:gr-qc/0106033. doi:10.1088/0264-9381/18/23/311.
References
- Coxeter, H.S.M; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
- Weisstein, Eric W., "Dihedron" from MathWorld.
- Dihedron
- Tetrahedron
- Pentahedron
- Hexahedron
- Heptahedron
- Octahedron
- Enneahedron
- Decahedron
- Dodecahedron
- Tetradecahedron
- Icosahedron
Polyhedron navigator Platonic solids (regular) Archimedean solids
(Semiregular/Uniform)Catalan solids
(Dual semiregular)triakis tetrahedron · rhombic dodecahedron · triakis octahedron · tetrakis cube · deltoidal icositetrahedron · disdyakis dodecahedron · pentagonal icositetrahedron · rhombic triacontahedron · triakis icosahedron · pentakis dodecahedron · deltoidal hexecontahedron · disdyakis triacontahedron · pentagonal hexecontahedronDihedral regular dihedron · hosohedronDihedral uniform Duals of dihedral uniform Dihedral others Degenerate polyhedra are in italics.Categories:
Wikimedia Foundation. 2010.
