- Dipole antenna
-
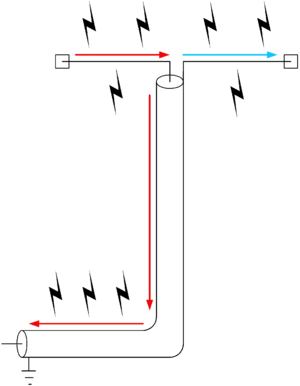
 A schematic of a half-wave dipole antenna connected to an unbalanced coaxial cable. Better practice is to connect the balanced dipole to the unbalanced line with a balun.
A schematic of a half-wave dipole antenna connected to an unbalanced coaxial cable. Better practice is to connect the balanced dipole to the unbalanced line with a balun.
A dipole antenna is a radio antenna that can be made of a simple wire, with a center-fed driven element. It consists of two metal conductors of rod or wire, oriented parallel and collinear with each other (in line with each other), with a small space between them. The radio frequency voltage is applied to the antenna at the center, between the two conductors. These antennas are the simplest practical antennas from a theoretical point of view. They are used alone as antennas, notably in traditional "rabbit ears" television antennas, and as the driven element in many other types of antennas, such as the Yagi. Dipole antennas were invented by German physicist Heinrich Hertz around 1886 in his pioneering experiments with radio waves.
Contents
Elementary doublet

An elementary doublet is a small length of conductor
 (small compared to the wavelength
(small compared to the wavelength  ) carrying an alternating current:
) carrying an alternating current:
Here
 is the angular frequency (and
is the angular frequency (and  the frequency), and
the frequency), and  is
is  , so that
, so that  is a phasor.
is a phasor.Note that this dipole cannot be physically constructed because the current needs somewhere to come from and somewhere to go to. In reality, this small length of conductor will be just one of the multiple segments into which we must divide a real antenna, in order to calculate its properties. The interest of this imaginary elementary antenna is that we can easily calculate the electrical far field of the electromagnetic wave radiated by each elementary doublet. We give just the result:

Where,
 is the far electric field of the electromagnetic wave radiated in the θ direction.
is the far electric field of the electromagnetic wave radiated in the θ direction. is the permittivity of vacuum.
is the permittivity of vacuum. is the speed of light in vacuum.
is the speed of light in vacuum. is the distance from the doublet to the point where the electrical field
is the distance from the doublet to the point where the electrical field  is evaluated.
is evaluated. is the wavenumber
is the wavenumber 
The exponent of
 accounts for the phase dependence of the electrical field on time and the distance from the dipole.
accounts for the phase dependence of the electrical field on time and the distance from the dipole.The far electric field
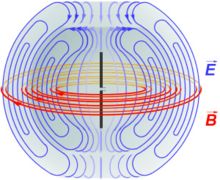
 of the electromagnetic wave is coplanar with the conductor and perpendicular with the line joining the dipole to the point where the field is evaluated. If the dipole is placed in the center of a sphere in the axis south-north, the electric field would be parallel to geographic meridians and the magnetic field of the electromagnetic wave would be parallel to geographic parallels.
of the electromagnetic wave is coplanar with the conductor and perpendicular with the line joining the dipole to the point where the field is evaluated. If the dipole is placed in the center of a sphere in the axis south-north, the electric field would be parallel to geographic meridians and the magnetic field of the electromagnetic wave would be parallel to geographic parallels.Near Field
The above formulas are valid for the far field of the antenna (
 ), and are the only contribution to the radiated field. The formulas in the near field have additional terms that reduce with r2 and r3. These are,
), and are the only contribution to the radiated field. The formulas in the near field have additional terms that reduce with r2 and r3. These are,


where
 . The energy associated with the term of the near field flows back and forward out and into the antenna.
. The energy associated with the term of the near field flows back and forward out and into the antenna.Short dipole
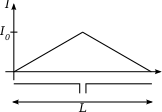
A short dipole is a physically feasible dipole formed by two conductors with a total length
 very small compared with the wavelength
very small compared with the wavelength  . The two conducting wires are fed at the centre of the dipole. We assume the hypothesis that the current is maximal at the centre (where the dipole is fed) and that it decreases linearly to be zero at the ends of the wires. Note that the direction of the current is the same in both the dipole branches - to the right in both or to the left in both. The far field
. The two conducting wires are fed at the centre of the dipole. We assume the hypothesis that the current is maximal at the centre (where the dipole is fed) and that it decreases linearly to be zero at the ends of the wires. Note that the direction of the current is the same in both the dipole branches - to the right in both or to the left in both. The far field  of the electromagnetic wave radiated by this dipole is:
of the electromagnetic wave radiated by this dipole is:


Emission is maximal in the plane perpendicular to the dipole and zero in the direction of wires which is the direction of the current. The emission diagram is circular section torus shaped (right image) with zero inner diameter. In the left image the doublet is vertical in the torus centre.Knowing this electric field, we can compute the total emitted power and then compute the resistive part of the series impedance of this dipole due to the radiated field, known as the radiation resistance:
 (for
(for  ).
).where Z0 is the impedance of free space. Using a common approximation of
 ohms, we get:
ohms, we get: ohms
ohmsAntenna gain
Antenna gain is the ratio of surface power radiated by the antenna to the surface power radiated by a hypothetical isotropic antenna:

The surface power carried by an electromagnetic wave is:

The surface power radiated by an isotropic antenna feed with the same power is:

Substituting values for the case of a short dipole, final result is:
 = 1.5 = 1.76 dBi
= 1.5 = 1.76 dBidBi simply means decibels gain, relative to an isotropic antenna.
Half-wave antenna

Typically a dipole antenna is formed by two quarter wavelength conductors or elements placed back to back for a total length of
 . A standing wave on an element of a length ~
. A standing wave on an element of a length ~ yields the greatest voltage differential, as one end of the element is at a node while the other is at an antinode of the wave. The larger the differential voltage, the greater the current between the elements.
yields the greatest voltage differential, as one end of the element is at a node while the other is at an antinode of the wave. The larger the differential voltage, the greater the current between the elements.
Assuming a sinusoidal distribution, the current impressed by this voltage differential is given by:

For the far-field case, the formula for the electric field of a radiating electromagnetic wave is somewhat more complex:

But the fraction
 is not very different from
is not very different from  .
.The resulting emission diagram is a slightly flattened torus.


The image on the left shows the section of the emission pattern. We have drawn, in dotted lines, the emission pattern of a short dipole. We can see that the two patterns are very similar. The image at right shows the perspective view of the same emission pattern.
This time it is not possible to compute analytically the total power emitted by the antenna (the last formula does not allow), though a simple numerical integration or series expansion leads to the more precise, actual value of the half-wave resistance:
![\begin{align}R_{\frac{\lambda}{2}}
&= \frac{Z_0}{2\pi}\left[\ln(2\pi\gamma)-\operatorname{Ci}(2\pi)\right]\approx 60\operatorname{Cin}(2\pi)= 60\left[\ln(2\pi\gamma)-\operatorname{Ci}(2\pi)\right]=120\int_{0}^{\frac{\pi}{2}}\frac{\cos\left(\frac{\pi}{2}\cos\theta\right)^2}{\sin\theta}d\theta,\\
&=15\left[2\pi^2-\frac{1}{3}\pi^4+\frac{4}{135}\pi^6-\frac{1}{630}\pi^8+\frac{4}{70875}\pi^{10}\ldots-(-1)^n\frac{(2\pi)^{2n}}{n(2n)!}\right],\\
&\approx 73.1 \Omega;
\end{align}\,\!](5/8457e1294aba4d3bfb9ca92cb4d687b5.png)
This leads to the gain of a dipole antenna,
 :
:The resistance, however, is not enough to characterize the dipole impedance, as there is also an imaginary part——it is better to measure the impedance.
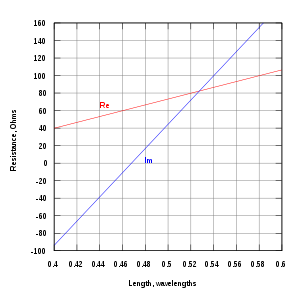
In the image below, the real and imaginary parts of a dipole's impedance are drawn for lengths going from
 to
to  , accompanied by a chart comparing the gains of dipole antennas of other lengths, both as a number and in dBi:
, accompanied by a chart comparing the gains of dipole antennas of other lengths, both as a number and in dBi:Gain of dipole antennas length L in 
Gain Gain(dBi)  0.1
0.11.50 1.76 0.5 1.64 2.15 Quarter-wave antenna
 The antenna and its image form a
The antenna and its image form a dipole that radiates only upward.
dipole that radiates only upward.The quarter wave monopole antenna is a single element antenna fed at one end, that behaves as a dipole antenna. It is formed by a conductor
 in length. It is fed in the lower end, which is near a conductive surface which works as a reflector (see Effect of ground). The current in the reflected image has the same direction and phase as the current in the real antenna. The quarter-wave conductor and its image together form a half-wave dipole that radiates only in the upper half of space.
in length. It is fed in the lower end, which is near a conductive surface which works as a reflector (see Effect of ground). The current in the reflected image has the same direction and phase as the current in the real antenna. The quarter-wave conductor and its image together form a half-wave dipole that radiates only in the upper half of space.In this upper side of space the emitted field has the same amplitude of the field radiated by a half-wave dipole fed with the same current. Therefore, the total emitted power is one-half the emitted power of a half-wave dipole fed with the same current. As the current is the same, the radiation resistance (real part of series impedance) will be one-half of the series impedance of a half-wave dipole. As the reactive part is also divided by 2, the impedance of a quarter wave antenna is
 ohms. Since the fields above ground are the same as for the dipole, but only half the power is applied, the gain is twice (3dB over) that for a half-wave dipole (
ohms. Since the fields above ground are the same as for the dipole, but only half the power is applied, the gain is twice (3dB over) that for a half-wave dipole ( ), that is 5.14 dBi.
), that is 5.14 dBi.The earth can be used as ground plane, but it is a poor conductor: the reflected antenna image is only clear at glancing angles (far from the antenna). At these glancing angles, electromagnetic fields and radiation patterns are thus the same as for a half-wave dipole.
Naturally, the impedance of the earth is far inferior to that of a good conductor ground plane -- this can be improved (at cost) by laying a copper mesh.
When ground is not available (such as in a vehicle) other metallic surfaces can serve as a ground plane (typically the vehicle's roof). Alternatively, radial wires placed at the base of the antenna can simulate a ground plane. For VHF bands, the radiating and ground-plane elements can be constructed from rigid rods or tubes.
Dipole characteristics
Frequency versus length
Dipoles that are much smaller than the wavelength of the signal are called Hertzian, short, or infinitesimal dipoles. These have a very low radiation resistance and a high reactance, making them inefficient, but they are often the only available antennas at very long wavelengths. Dipoles whose length is half the wavelength of the signal are called half-wave dipoles, and are more efficient. In general radio engineering, the term dipole usually means a half-wave dipole (center-fed).
A half-wave dipole is cut to length l for frequency f MHz according to the formula
 where l is in metres or
where l is in metres or  where l is in feet.[1] This is because the impedance of the dipole is purely resistive at about this length. The length of the dipole antenna is approximately 95% of half a wavelength at the speed of light in free space. The exact value depends on the ratio of the wire radius to wavelength, as the reactance of a dipole depends on the ratio of wire radius to wavelength. For thin wires (radius = 0.000001 wavelengths, this is approximately 98.1%, dropping to 91.5% for thick wires (radius = 0.01 wavelengths).
where l is in feet.[1] This is because the impedance of the dipole is purely resistive at about this length. The length of the dipole antenna is approximately 95% of half a wavelength at the speed of light in free space. The exact value depends on the ratio of the wire radius to wavelength, as the reactance of a dipole depends on the ratio of wire radius to wavelength. For thin wires (radius = 0.000001 wavelengths, this is approximately 98.1%, dropping to 91.5% for thick wires (radius = 0.01 wavelengths).The magic numbers above are derived from a one Hz wavelength which is the distance that light radio travels in one second. Speed of light in vacuum is 299,792,458 m/s, which is divided by 1 million to account for MHz rather than Hz, which is then divided by 2 for a half-wave dipole antenna. A fudge factor of approximately 0.95 is multiplied to account for the fact the input reactance of a dipole is inductive when exactly 0.5 wavelengths long, but the reactance reduces to 0 (i.e. the dipole becomes resonanate) at a length of approximately 0.475 wavelengths, which results in the magic number of 143 m·MHz or 468 ft·MHz. But as noted above, a more accurate calculation would need to take into account the wire radius. Such a calculation is quite complex.
Radiation pattern and gain
Dipoles have an radiation pattern, shaped like a toroid (doughnut) symmetrical about the axis of the dipole. The radiation is maximum at right angles to the dipole, dropping off to zero on the antenna's axis. The theoretical maximum gain of a Hertzian dipole is 10 log 1.5 or 1.76 dBi. The maximum theoretical gain of a λ/2-dipole is 10 log 1.64 or 2.15 dBi.
 Radiation pattern of a half-wave dipole antenna. The scale is linear.
Radiation pattern of a half-wave dipole antenna. The scale is linear. Gain of a half-wave dipole (same as left). The scale is in dBi (decibels over isotropic).
Gain of a half-wave dipole (same as left). The scale is in dBi (decibels over isotropic).Feeder line
Ideally, a half-wave (λ/2) dipole should be fed with a balanced line matching the theoretical 73 ohm impedance of the antenna. A folded dipole uses a 300 ohm balanced feeder line.
Many people have had success in feeding a dipole directly with a coaxial cable feed rather than a ladder-line. However, coax is not symmetrical and thus not a balanced feeder. It is unbalanced, because the outer shield is connected to earth potential at the other end. When a balanced antenna such as a dipole is fed with an unbalanced feeder, common mode currents can cause the coax line to radiate in addition to the antenna itself, and the radiation pattern may be asymmetrically distorted. This can be remedied with the use of a balun.
Common applications
Set-top TV antenna
The most common dipole antenna is the type used with televisions, often colloquially referred to as "rabbit ears" or "bunny ears". While in most applications the dipole elements are arranged along the same line, rabbit ears are adjustable in length and angle. Larger dipoles are sometimes hung in a V shape with the center near the radio equipment on the ground or the ends on the ground with the center supported. Shorter dipoles can be hung vertically. Some have extra elements to get better reception such as loops (especially for UHF transmissions), which can be turnable around a vertical axis, or a dial, which modifies the electrical properties of the antenna at each dial position.
Folded dipole
Another common place one can see dipoles is as antennas for the FM band - these are folded dipoles. The tips of the antenna are folded back until they almost meet at the feedpoint, such that the antenna comprises one entire wavelength. This arrangement has a greater bandwidth than a standard half-wave dipole. If the conductor has a constant radius and cross-section, at resonance the input impedance is four times that of a half-wave dipole.
Shortwave antenna
Dipoles for longer wavelengths are made from solid or stranded wire. Portable dipole antennas are made from wire that can be rolled up when not in use. Ropes with weights on the ends can be thrown over supports such as tree branches and then used to hoist up the antenna. The center and the connecting cable can be hoisted up with the ends on the ground or the ends hoisted up between two supports in a V shape. While permanent antennas can be trimmed to the proper length, it is helpful if portable antennas are adjustable to allow for local conditions when moved. One easy way is to fold the ends of the elements to form loops and use adjustable clamps. The loops can then be used as attachment points.
It is important to fit a good insulator at the ends of the dipole, as failure to do so can lead to a flashover if the dipole is used with a transmitter. Various purchased or improvised insulators can be used.
Whip antenna
The whip antenna is probably the most common and simplest-looking antenna. These are monopoles, and the most common and practical is the quarter-wave monopole which could be considered as half of a dipole using a ground plane as the image of the other half. The commonly referred-to end-fed dipole is actually just a half-wave monopole whip antenna.
Dipoles versus whip antennas
Dipoles are generally more efficient than whip antennas (quarter-wave monopoles). The total radiated power and the radiation resistance are twice that of a quarter-wave monopole. Thus, if a whip antenna were used with an infinite perfectly conducting ground plane, then it would be as efficient in half-space as a dipole in free space an infinite distance from any conductive surfaces such as the earth's surface.
Dipole towers
Large constructed half-wavelength dipole towers include the Warsaw radio mast — the only half-wave dipole for longwave ever built — and Blaw-Knox Towers.
Military
US Military personnel occasionally use a 'doublet' antenna,[2] especially during dismounted unconventional warfare. A radio operator may choose to bring several doublet antennas for different frequencies, such as an antenna cut to length for the set MEDEVAC (medical evacuation) frequency, NCS (net control station) frequency, and tactical frequency (the frequency used by troops in the field). This approach may not be acceptable depending on the mission. Note that a doublet antenna will not work with the standard SINCGARS radio when using frequency hopping(FH) but is effective for single channel (SC). A doublet antenna is more practical for radios not intended for FH.
Collinear antenna systems based on dipoles
Dipoles can be stacked end to end in phased arrays to make collinear antenna arrays, which exhibit more gain in certain directions—the toroidal radiation pattern is flattened out, giving maximum gain at right angles to the axis of the colinear array.
Slim Jim or J-Pole
A Slim Jim or J-pole is a form of end-fed dipole connected to a quarter-wave stub matching section.
Dipole types
Ideal half-wavelength dipole
This type of antenna is a special case where each wire is exactly one-quarter of the wavelength, for a total of a half wavelength. The radiation resistance is about 73 ohms if wire diameter is ignored, making it easily matched to a coaxial transmission line. The directivity is a constant 1.64, or 2.15 dB. Actual gain will be a little less due to ohmic losses.
If the dipole is not driven at the centre then the feed point resistance will be higher. If the feed point is distance x from one end of a half wave (λ/2) dipole, the resistance will be described by the following equation.
If taken to the extreme then the feed point resistance of a λ/2 long rod is infinite, but it is possible to use a λ/2 pole as an aerial; the right way to drive it is to connect it to one terminal of a parallel LC resonant circuit. The other side of the circuit must be connected to the braid of a coaxial cable lead and the core of the coaxial cable can be connected part way up the coil from the RF ground side. An alternative means of feeding this system is to use a second coil which is magnetically coupled to the coil attached to the aerial.
Folded dipole
A folded dipole is a half-wave dipole with an additional wire connecting its two ends. If the additional wire has the same diameter and cross-section as the dipole, two nearly identical radiating currents are generated. The resulting far-field emission pattern is nearly identical to the one for the single-wire dipole described above; however, at resonance its input (feedpoint) impedance Rfd is four times the radiation resistance of a single-wire dipole. This is because for a fixed amount of power, the total radiating current I0 is equal to twice the current in each wire and thus equal to twice the current at the feed point. Equating the average radiated power to the average power delivered at the feedpoint, we may write
It follows that
The folded dipole is therefore well matched to 300-Ohm balanced transmission lines.
Hertzian dipole (current element)
The Hertzian dipole is a theoretical short dipole (significantly smaller than the wavelength) with a uniform current along its length. A true Hertzian dipole cannot physically exist, since the assumed current distribution implies an infinite charge density at its ends, and significant radiation requires a very high current over its very short length.
The radiation resistance is given by:
where Z0 is the impedance of free space. This is precisely four times the radiation resistance of the real short dipole with the linearly tapered current distribution.
The radiation resistance is typically a fraction of an ohm, making a real infinitesimal dipole an inefficient radiator. The directivity D, which is the theoretical gain of the antenna assuming no ohmic losses (not real-world), is a constant of 1.5, which corresponds to 1.76 dB. Actual gain will be much less due to the ohmic losses (because of the very high currents) and the loss inherent in connecting a transmission line to the antenna, which is very hard to do efficiently considering the incredibly low radiation resistance. The maximum effective aperture is:
or
A surprising result is that even though the Hertzian dipole is minute, its effective aperture is comparable to antennas many times its size. A real small antenna will have a smaller effective aperture, because of its lower gain.
Dipole as a reference standard
Antenna gain is sometimes measured as "x dB above a dipole", which means that the antenna in question is being compared to a dipole, and has x dB more gain (has more directivity) than the dipole tuned to the same operating frequency. In this case one says the antenna has a gain of "x dBd" (see decibel). More often, gains are expressed relative to an isotropic radiator, which is an imaginary aerial that radiates equally in all directions. In this case one uses dBi instead of dBd (see decibel). As it is impossible to build an isotropic radiator, gain measurements expressed relative to a dipole are more practical when a reference dipole aerial is used for experimental measurements. 0 dBd is often considered equal to 2.15 dBi.
From Babinet's principle, a dipole antenna is complementary to a slot antenna consisting of a slot the same size and shape as a dipole cut from an infinite sheet of metal; both give the same radiation pattern.
Dipole with baluns
A dipole, being composed of two symmetrical ungrounded elements, works best when fed by a balanced transmission line, such as ladder line. When a dipole with an unbalanced feedline such as coaxial cable is used for transmitting, the shield side of the cable, in addition to the antenna, radiates. This can induce RF currents into other electronic equipment near the radiating feedline, causing RF interference. Furthermore, the antenna is not as efficient as it could be because it is radiating closer to the ground and its radiation (and reception) pattern may be distorted asymmetrically. At higher frequencies, where the length of the dipole becomes significantly shorter than the diameter of the feeder coax, this becomes a more significant problem. To prevent this, dipoles fed by coaxial cables have a balun between the cable and the antenna, to convert the unbalanced signal provided by the coax to a balanced symmetrical signal for the antenna.
Several types of baluns are commonly used to transmit on a dipole: current baluns and coax baluns.
Current balun
A current balun is a bit more expensive but has the characteristic of being more broadband.[2] It can also be as simple as winding the coax cable over a ferrite core.[3] Or nothing but coax cable:[4]
Coax balun
A coax balun is a cost effective method to eliminate feeder radiation, but is limited to a narrow set of operating frequencies.
- One easy way to make a balun is a (λ/2) length of coaxial cable. The inner core of the cable is linked at each end to one of the balanced connections for a feeder or dipole. One of these terminals should be connected to the inner core of the coaxial feeder. All three braids should be connected together. This then forms a 4:1 balun which works correctly at only a narrow band of frequencies.
Sleeve balun
At VHF frequencies, a sleeve balun can also be built to remove feeder radiation.[3]
- Another narrow band design is to use a λ/4 length of metal pipe. The coaxial cable is placed inside the pipe; at one end the braid is wired to the pipe while at the other end no connection is made to the pipe. The balanced end of this balun is at the end where the pipe is wired to the braid. The λ/4 conductor acts as a transformer converting the infinite impedance at the unconnected end into a zero impedance at the end connected to the braid. Hence any current entering the balun through the connection, which goes to the braid at the end with the connection to the pipe, will flow into the pipe. This balun design is impractical for low frequencies because of the long length of pipe that will be needed.
See also
- Electronic symbol
- isotropic antenna
- omnidirectional antenna
- whip antenna
- driven element
- balun
- Coaxial antenna
- amateur radio
- shortwave listening
- T-aerial
- AM broadcasting
- FM broadcasting
References
- ^ [1]
- ^ doublet antenna globalsecurity.org
- ^ Sleeve Baluns
Elementary, short and half-wave dipoles:
- Terman, Federick R.; Helliwell, Robert (1955), Electronic Radio and Engineering (4th ed.), MacGraw-Hill, ISBN 978-0070857957
- Feynman; Leighton; Sands, Lectures on Physics, Addison-Wesley
- Panofsky, W.; Phillips, M., Classical Electricity and Magnetism, Addison-Wesley
- http://www.ece.rutgers.edu/~orfanidi/ewa/ Electromagnetic Waves and Antennas, Sophocles J. Orfanidis.
- Wire Antenna Resources for Ham Radio Wire Antenna Resources including off center fed dipole (OCFD), dipole calculators and construction sites
- http://stewks.ece.stevens-tech.edu/sktpersonal.dir/sktwireless/lin-ant.pdf
- http://www.nt.hs-bremen.de/peik/asc/asc_antenna_slides.pdf
- The Hertzian dipole
- The ARRL Antenna Book (21st ed.), The American Radio Relay League, Inc., 2007, ISBN 0-87259-987-6, http://www.arrl.org/catalog/?category=Antennas,+Transmission+Lines+%26+Propagation#6133
- ARRL's Wire Antenna Classics - A collection of the best articles from ARRL publications, 1 (First ed.), The American Radio Relay League, Inc., 2005, ISBN 0-87259-707-5, http://www.arrl.org/catalog/?category=Antennas,+Transmission+Lines+%26+Propagation#7075
- Reflections on Hertz and the Hertzian Dipole Jed Z. Buchwald, MIT and the Dibner Institute for the History of Science and Technology (link inactive February 2, 2007; archive accessed from Wayback, March 13, 2011)
External links
- Dipole Antenna Tutorial EM Talk
- Broadband Dipoles Antenna-Theory.com
- AC6V's Homebrew Antennas Links
- Your First HF Dipole - simple yet complete tutorial from eham.net
Antenna types Isotropic Omnidirectional Coaxial antenna · Dipole antenna · Discone antenna · Folded unipole antenna · Ground-plane antenna · Halo antenna · Helical antenna · J-pole antenna · Mast radiator · Monopole antenna · Random wire antenna · Rubber Ducky antenna · T2FD Antenna · Whip antennaDirectional AWX antenna · Beverage antenna · Cantenna · Collinear antenna · Fractal antenna · Ground dipole · Helical antenna · Horizontal curtain · Horn · Inverted vee antenna · Log-periodic antenna · Loop antenna · Microstrip antenna · Patch antenna · Phased array · Parabolic antenna · Plasma antenna · Quad antenna · Reflective array antenna · Regenerative loop antenna · Rhombic antenna · Sector antenna · Short backfire antenna · Slot antenna · Turnstile antenna · Vivaldi-antenna · Yagi-Uda antennaApplication-specific Analogue television broadcasting topics Systems Color systems Video Back porch and front porch • Black level • Chrominance • Chrominance subcarrier • Colorburst • Color killer • Color TV • Composite video • Frame (video) • Horizontal scan rate • Horizontal blanking interval • Luma • Nominal analogue blanking • Overscan • Raster scan • Safe area • Television lines • Vertical blanking interval • White clipperSound Modulation Transmission Amplifiers • Antenna (radio) • Cavity amplifier • Differential gain • Differential phase • Diplexer • Dipole antenna • Dummy load • Frequency mixer • Intercarrier method • Intermediate frequency • Output power of an analog TV transmitter • Pre-emphasis • Residual carrier • Split sound system • Superheterodyne transmitter • Television receive-only • Television transmitter • Terrestrial television • Transmitter station • TransposerFrequencies & Bands Propagation Beam tilt • Distortion • Earth bulge • Field strength in free space • Knife-edge effect • Noise (electronics) • Null fill • Path loss • Radiation pattern • Skew • Television interferenceTesting Distortionmeter • Field strength meter • Vectorscope • VIT signals • Zero reference pulseArtifacts Categories:- Radio frequency antenna types
- Radio technology
Wikimedia Foundation. 2010.