- Simplex
-
For other uses, see Simplex (disambiguation).
 A regular 3-simplex or tetrahedron
A regular 3-simplex or tetrahedron
In geometry, a simplex (plural simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron, and a 4-simplex is a pentachoron. A single point may be considered a 0-simplex, and a line segment may be considered a 1-simplex. A simplex may be defined as the smallest convex set containing the given vertices.
A regular simplex[1] is a simplex that is also a regular polytope. A regular n-simplex may be constructed from a regular (n − 1)-simplex by connecting a new vertex to all original vertices by the common edge length.
In topology and combinatorics, it is common to “glue together” simplices to form a simplicial complex. The associated combinatorial structure is called an abstract simplicial complex, in which context the word “simplex” simply means any finite set of vertices.
Contents
Elements
The convex hull of any nonempty subset of the n+1 points that define an n-simplex is called a face of the simplex. Faces are simplices themselves. In particular, the convex hull of a subset of size m+1 (of the n+1 defining points) is an m-simplex, called an m-face of the n-simplex. The 0-faces (i.e., the defining points themselves as sets of size 1) are called the vertices (singular: vertex), the 1-faces are called the edges, the (n − 1)-faces are called the facets, and the sole n-face is the whole n-simplex itself. In general, the number of m-faces is equal to the binomial coefficient
 . Consequently, the number of m-faces of an n-simplex may be found in column (m + 1) of row (n + 1) of Pascal's triangle. A simplex A is a coface of a simplex B if B is a face of A. Face and facet can have different meanings when describing types of simplices in a simplicial complex. See Simplicial complex#Definitions
. Consequently, the number of m-faces of an n-simplex may be found in column (m + 1) of row (n + 1) of Pascal's triangle. A simplex A is a coface of a simplex B if B is a face of A. Face and facet can have different meanings when describing types of simplices in a simplicial complex. See Simplicial complex#DefinitionsThe regular simplex family is the first of three regular polytope families, labeled by Coxeter as αn, the other two being the cross-polytope family, labeled as βn, and the hypercubes, labeled as γn. A fourth family, the infinite tessellation of hypercubes, he labeled as δn.
The number of 1-faces (edges) of the n-simplex is the (n-1)th triangle number, the number of 2-faces (faces) of the n-simplex is the (n-2)th tetrahedron number, the number of 3-faces (cells) of the n-simplex is the (n-3)th pentachoron number, and so on.
n-Simplex elements[2] Δn Name Schläfli symbol
Coxeter-Dynkin0-
faces
(vertices)1-
faces
(edges)2-
faces
(faces)3-
faces
(cells)4-
faces
5-
faces
6-
faces
7-
faces
8-
faces
9-
faces
10-
faces
Sum
=2n+1-1Δ0 0-simplex
(point)1 1 Δ1 1-simplex
(line segment){}

2 1 3 Δ2 2-simplex
(triangle){3}



3 3 1 7 Δ3 3-simplex
(tetrahedron){3,3}





4 6 4 1 15 Δ4 4-simplex
(pentachoron){3,3,3}







5 10 10 5 1 31 Δ5 5-simplex
(hexateron){3,3,3,3}









6 15 20 15 6 1 63 Δ6 6-simplex
(heptapeton){3,3,3,3,3}











7 21 35 35 21 7 1 127 Δ7 7-simplex
(octaexon){3,3,3,3,3,3}













8 28 56 70 56 28 8 1 255 Δ8 8-simplex
(enneazetton){3,3,3,3,3,3,3}















9 36 84 126 126 84 36 9 1 511 Δ9 9-simplex
(decayotton){3,3,3,3,3,3,3,3}

















10 45 120 210 252 210 120 45 10 1 1023 Δ10 10-simplex
(hendecaxennon){3,3,3,3,3,3,3,3,3}



















11 55 165 330 462 462 330 165 55 11 1 2047 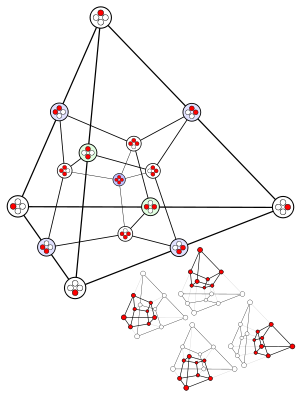 The sum of hyperfaces is always a power of two minus one. This figure (a projection of the tesseract) shows the midpoints of the 15 hyperfaces of the tetrahedron.
The sum of hyperfaces is always a power of two minus one. This figure (a projection of the tesseract) shows the midpoints of the 15 hyperfaces of the tetrahedron.
 The numbers of hyperfaces in the above table are the same as in Pascal's triangle, without the left diagonal.
The numbers of hyperfaces in the above table are the same as in Pascal's triangle, without the left diagonal.
In some conventions,[who?] the empty set is defined to be a (−1)-simplex. The definition of the simplex above still makes sense if n = −1. This convention is more common in applications to algebraic topology (such as simplicial homology) than to the study of polytopes.
Symmetric graphs of regular simplices
These Petrie polygon (skew orthogonal projections) show all the vertices of the regular simplex on a circle, and all vertex pairs connected by edges.
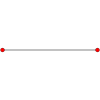
1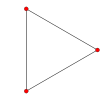
2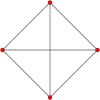
3
4
5
6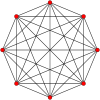
7
8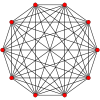
9
10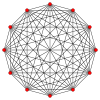
11
12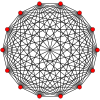
13
14
15
16
17
18
19
20The standard simplex
The standard n-simplex (or unit n-simplex) is the subset of Rn+1 given by
The simplex Δn lies in the affine hyperplane obtained by removing the restriction ti ≥ 0 in the above definition. The standard simplex is clearly regular.
The n+1 vertices of the standard n-simplex are the points {ei} ⊂ Rn+1, where
- e0 = (1, 0, 0, ..., 0),
- e1 = (0, 1, 0, ..., 0),

- en = (0, 0, 0, ..., 1).
There is a canonical map from the standard n-simplex to an arbitrary n-simplex with vertices (v0, …, vn) given by
The coefficients ti are called the barycentric coordinates of a point in the n-simplex. Such a general simplex is often called an affine n-simplex, to emphasize that the canonical map is an affine transformation. It is also sometimes called an oriented affine n-simplex to emphasize that the canonical map may be orientation preserving or reversing.
More generally, there is a canonical map from the standard (n − 1)-simplex (with n vertices) onto any polytope with n vertices, given by the same equation (modifying indexing):
These are known as generalized barycentric coordinates, and express every polytope as the image of a simplex:

Increasing coordinates
An alternative coordinate system is given by taking the indefinite sum:
This yields the alternative presentation by order, namely as nondecreasing n-tuples between 0 and 1:
Geometrically, this is an n-dimensional subset of
 (maximal dimension, codimension 0) rather than of
(maximal dimension, codimension 0) rather than of  (codimension 1). The hyperfaces, which on the standard simplex correspond to one coordinate vanishing, ti = 0, here correspond to successive coordinates being equal, si = si + 1, while the interior corresponds to the inequalities becoming strict (increasing sequences).
(codimension 1). The hyperfaces, which on the standard simplex correspond to one coordinate vanishing, ti = 0, here correspond to successive coordinates being equal, si = si + 1, while the interior corresponds to the inequalities becoming strict (increasing sequences).A key distinction between these presentations is the behavior under permuting coordinates – the standard simplex is stabilized by permuting coordinates, while permuting elements of the "ordered simplex" do not leave it invariant, as permuting an ordered sequence generally makes it unordered. Indeed, the ordered simplex is a (closed) fundamental domain for the action of the symmetric group on the n-cube, meaning that the orbit of the ordered simplex under the n! elements of the symmetric group divides the n-cube into n! mostly disjoint simplices (disjoint except for boundaries), showing that this simplex has volume 1 / n! Alternatively, the volume can be computed by an iterated integral, whose successive integrands are

A further property of this presentation is that it uses the order but not addition, and thus can be defined in any dimension over any ordered set, and for example can be used to define an infinite-dimensional simplex without issues of convergence of sums.
Projection onto the standard simplex
Especially in numerical applications of probability theory a projection onto the standard simplex is of interest. Given
 with possibly negative entries, the closest point
with possibly negative entries, the closest point  on the simplex has coordinates
on the simplex has coordinateswhere Δ is chosen such that

Corner of cube
Finally, a simple variant is to replace "summing to 1" with "summing to at most 1"; this raises the dimension by 1, so to simplify notation, the indexing changes:
This yields an n-simplex as a corner of the n-cube, and is a standard orthogonal simplex. This is the simplex used in the simplex method, which is based at the origin, and locally models a vertex on a polytope with n faces.
Cartesian coordinates for regular n-dimensional simplex in Rn
The coordinates of the vertices of a regular n-dimensional simplex can be obtained from these two properties,
- For a regular simplex, the distances of its vertices to its center are equal.
- The angle subtended by any two vertices of an n-dimensional simplex through its center is

These can be used as follows. Let vectors (v0, v1, ..., vn) represent the vertices of an n-simplex center the origin, all unit vectors so a distance 1 from the origin, satisfying the first property. The second property means the dot product between any pair of the vectors is -1⁄n. This can be used to calculate positions for them.
For example in three dimensions the vectors (v0, v1, v2, v3) are the vertices of a 3-simplex or tetrahedron. Write these as
Choose the first vector v0 to have all but the first component zero, so by the first property it must be (1, 0, 0) and the vectors become
By the second property the dot product of v0 with all other vectors is -1⁄3, so each of their x components must equal this, and the vectors become
Next choose v1 to have all but the first two elements zero. The second element is the only unknown. It can be calculated from the first property using the Pythagorean theorem (choose any of the two square roots), and so the second vector can be completed:
The second property can be used to calculate the remaining y components, by taking the dot product of v1 with each and solving to give
From which the z components can be calculated, using the Pythagorean theorem again to satisfy the first property, the two possible square roots giving the two results
This process can be carried out in any dimension, using n + 1 vectors, applying the first and second properties alternately to determine all the values.
Geometric properties
The oriented volume of an n-simplex in n-dimensional space with vertices (v0, ..., vn) is
where each column of the n × n determinant is the difference between the vectors representing two vertices. Without the 1/n! it is the formula for the volume of an n-parallelepiped. One way to understand the 1/n! factor is as follows. If the coordinates of a point in a unit n-box are sorted, together with 0 and 1, and successive differences are taken, then since the results add to one, the result is a point in an n simplex spanned by the origin and the closest n vertices of the box. The taking of differences was a unimodular (volume-preserving) transformation, but sorting compressed the space by a factor of n!.
The volume under a standard n-simplex (i.e. between the origin and the simplex in Rn+1) is
The volume of a regular n-simplex with unit side length is
as can be seen by multiplying the previous formula by xn+1, to get the volume under the n-simplex as a function of its vertex distance x from the origin, differentiating with respect to x, at
 (where the n-simplex side length is 1), and normalizing by the length
(where the n-simplex side length is 1), and normalizing by the length  of the increment,
of the increment,  , along the normal vector.
, along the normal vector.The dihedral angle of a regular n-dimensional simplex is cos−1(1/n).[3][4]
Simplexes with an "orthogonal corner"
Orthogonal corner means here, that there is a vertex at which all adjacent hyperfaces are pairwise orthogonal. Such simplexes are generalizations of right angle triangles and for them there exists a n-dimensional version of the Pythagorean theorem:
The sum of the squared (n-1)-dimensional volumes of the hyperfaces adjacent to the orthogonal corner equals the squared (n-1)-dimensional volume of the hyperface opposite of the orthogonal corner.
where
 are hyperfaces being pairwise orthogonal to each other but not orthogonal to A0, which is the hyperface opposite of the orthogonal corner.
are hyperfaces being pairwise orthogonal to each other but not orthogonal to A0, which is the hyperface opposite of the orthogonal corner.For a 2-simplex the theorem is the Pythagorean theorem for triangles with a right angle and for a 3-simplex it is de Gua's theorem for a tetrahedron with a cube corner.
Relation to the (n+1)-hypercube
The Hasse diagram of the face lattice of an n-simplex is isomorphic to the graph of the (n+1)-hypercube's edges, with the hypercube's vertices mapping to each of the n-simplex's elements, including the entire simplex and the null polytope as the extreme points of the lattice (mapped to two opposite vertices on the hypercube). This fact may be used to efficiently enumerate the simplex's face lattice, since more general face lattice enumeration algorithms are more computationally expensive.
The n-simplex is also the vertex figure of the (n+1)-hypercube. It is also the facet of the (n+1)-orthoplex.
Topology
Topologically, an n-simplex is equivalent to an n-ball. Every n-simplex is an n-dimensional manifold with boundary.
Probability
Main article: Categorical distributionIn probability theory, the points of the standard n-simplex in (n + 1)-space are the space of possible parameters (probabilities) of the categorical distribution on n+1 possible outcomes.
Algebraic topology
In algebraic topology, simplices are used as building blocks to construct an interesting class of topological spaces called simplicial complexes. These spaces are built from simplices glued together in a combinatorial fashion. Simplicial complexes are used to define a certain kind of homology called simplicial homology.
A finite set of k-simplexes embedded in an open subset of Rn is called an affine k-chain. The simplexes in a chain need not be unique; they may occur with multiplicity. Rather than using standard set notation to denote an affine chain, it is instead the standard practice to use plus signs to separate each member in the set. If some of the simplexes have the opposite orientation, these are prefixed by a minus sign. If some of the simplexes occur in the set more than once, these are prefixed with an integer count. Thus, an affine chain takes the symbolic form of a sum with integer coefficients.
Note that each face of an n-simplex is an affine n-1-simplex, and thus the boundary of an n-simplex is an affine n-1-chain. Thus, if we denote one positively-oriented affine simplex as
- σ = [v0,v1,v2,...,vn]
with the vj denoting the vertices, then the boundary
 of σ is the chain
of σ is the chain![\partial\sigma = \sum_{j=0}^n
(-1)^j [v_0,...,v_{j-1},v_{j+1},...,v_n]](2/8f27d29fd4e69e76238239bed198884f.png) .
.
More generally, a simplex (and a chain) can be embedded into a manifold by means of smooth, differentiable map
 . In this case, both the summation convention for denoting the set, and the boundary operation commute with the embedding. That is,
. In this case, both the summation convention for denoting the set, and the boundary operation commute with the embedding. That is,where the ai are the integers denoting orientation and multiplicity. For the boundary operator
 , one has:
, one has:where ρ is a chain. The boundary operation commutes with the mapping because, in the end, the chain is defined as a set and little more, and the set operation always commutes with the map operation (by definition of a map).
A continuous map
 to a topological space X is frequently referred to as a singular n-simplex.
to a topological space X is frequently referred to as a singular n-simplex.Applications
Simplices are used in plotting quantities that sum to 1, such as proportions of subpopulations, as in a ternary plot.
In industrial statistics, simplices arise in problem formulation and in algorithmic solution. In the design of bread, the producer must combine yeast, flour, water, sugar, etc. In such mixtures, only the relative proportions of ingredients matters: For an optimal bread mixture, if the flour is doubled then the yeast should be doubled. Such mixture problem are often formulated with normalized constraints, so that the nonnegative components sum to one, in which case the feasible region forms a simplex. The quality of the bread mixtures can be estimated using response surface methodology, and then a local maximum can be computed using a nonlinear programming method, such as sequential quadratic programming.[5]
In operations research, linear programming problems can be solved by the simplex algorithm of George Dantzig.
In geometric design and computer graphics, many methods first perform simplicial triangulations of the domain and then fit interpolating polynomials to each simplex.[6]
See also
- Causal dynamical triangulation
- Distance geometry
- Delaunay triangulation
- Hill tetrahedron
- Other regular n-polytopes
- Polytope
- Metcalfe's Law
- List of regular polytopes
- Schläfli orthoscheme
- Simplex algorithm - a method for solving optimisation problems with inequalities.
- Simplicial complex
- Simplicial homology
- Simplicial set
- Ternary plot
- 3-sphere
Notes
- ^ Elte, E. L. (1912), The Semiregular Polytopes of the Hyperspaces, Groningen: University of Groningen Chapter IV, five dimensional semiregular polytope
- ^ (sequence A135278 in OEIS)
- ^ Harold R. Parks; Dean C. Wills (October 2002). "An Elementary Calculation of the Dihedral Angle of the Regular n-Simplex". The American Mathematical Monthly (Mathematical Association of America) 109 (8): 756–758. http://www.jstor.org/stable/3072403.
- ^ Harold R. Parks; Dean C. Wills (June 2009). Connections between combinatorics of permutations and algorithms and geometry. Oregon State University. http://ir.library.oregonstate.edu/xmlui/handle/1957/11929.
- ^ Cornell, John (2002). Experiments with Mixtures: Designs, Models, and the Analysis of Mixture Data (third ed.). Wiley. ISBN 0471079162.
- ^ Vondran, Gary L. (April 1998). "Radial and Pruned Tetrahedral Interpolation Techniques" (PDF). HP Technical Report HPL-98-95: 1–32. http://www.hpl.hp.com/techreports/98/HPL-98-95.pdf.
References
- Walter Rudin, Principles of Mathematical Analysis (Third Edition), (1976) McGraw-Hill, New York, ISBN 0-07-054235-X (See chapter 10 for a simple review of topological properties.).
- Andrew S. Tanenbaum, Computer Networks (4th Ed), (2003) Prentice Hall, ISBN 0-13-066102-3 (See 2.5.3).
- Luc Devroye, Non-Uniform Random Variate Generation. (1986) ISBN 0-387-96305-7; Web version freely downloadable.
- H.S.M. Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8
- p120-121
- p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n>=5)
- Weisstein, Eric W., "Simplex" from MathWorld.
External links
- Olshevsky, George, Simplex at Glossary for Hyperspace.
- OEIS sequence
 A135278 Triangle read by rows, giving the numbers T(n,m) = binomial(n+1,m+1); or, Pascal's triangle
A135278 Triangle read by rows, giving the numbers T(n,m) = binomial(n+1,m+1); or, Pascal's triangle  A007318 with its left-hand edge removed.
A007318 with its left-hand edge removed.
Dimension Dimensional spaces One · Two · Three · Four · Five · Six · Seven · Eight · n-dimensions · Spacetime · Projective space · Hyperplane
Polytopes and Shapes Concepts and mathematics Cartesian coordinates · Linear algebra · Geometric algebra · Conformal geometry · Reflection · Rotation · Plane of rotation · Space · Fractal dimension · MultiverseCategory Fundamental convex regular and uniform polytopes in dimensions 2–10 Family An BCn Dn E6 / E7 / E8 / F4 / G2 Hn Regular polygon Triangle Square Hexagon Pentagon Uniform polyhedron Tetrahedron Octahedron • Cube Demicube Dodecahedron • Icosahedron Uniform polychoron 5-cell 16-cell • Tesseract Demitesseract 24-cell 120-cell • 600-cell Uniform 5-polytope 5-simplex 5-orthoplex • 5-cube 5-demicube Uniform 6-polytope 6-simplex 6-orthoplex • 6-cube 6-demicube 122 • 221 Uniform 7-polytope 7-simplex 7-orthoplex • 7-cube 7-demicube 132 • 231 • 321 Uniform 8-polytope 8-simplex 8-orthoplex • 8-cube 8-demicube 142 • 241 • 421 Uniform 9-polytope 9-simplex 9-orthoplex • 9-cube 9-demicube Uniform 10-polytope 10-simplex 10-orthoplex • 10-cube 10-demicube n-polytopes n-simplex n-orthoplex • n-cube n-demicube 1k2 • 2k1 • k21 pentagonal polytope Topics: Polytope families • Regular polytope • List of regular polytopes Categories:- Polytopes
- Topology
- Multi-dimensional geometry
Wikimedia Foundation. 2010.




















