- Minor (graph theory)
-
In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G.
The theory of graph minors began with Wagner's theorem that a graph is planar if and only if it does not contain the complete graph K5 nor the complete bipartite graph K3,3 as a minor.[1] The Robertson-Seymour theorem states that the relation "being a minor of" is a well-quasi-ordering on the isomorphism classes of graphs, and implies that many other families of graphs have forbidden minor characterizations similar to that for the planar graphs.[2]
Contents
Definitions
An edge contraction is an operation which removes an edge from a graph while simultaneously merging together the two vertices it used to connect. An undirected graph H is a minor of another undirected graph G if a graph isomorphic to H can be obtained from G by contracting some edges, deleting some edges, and deleting some isolated vertices. The order in which a sequence of such contractions and deletions is performed on G does not affect the resulting graph H.
Graph minors are often studied in the more general context of matroid minors. In this context, it is common to assume that all graphs are connected, with self-loops and multiple edges allowed (that is, they are multigraphs rather than simple graphs; the contraction of a loop and the deletion of a cut-edge are forbidden operations. This point of view has the advantage that edge deletions leave the rank of a graph unchanged, and edge contractions always reduce the rank by one.
In other contexts (such as with the study of pseudoforests) it makes more sense to allow the deletion of a cut-edge, and to allow disconnected graphs, but to forbid multigraphs. In this variation of graph minor theory, a graph is always simplified after any edge contraction to eliminate its self-loops and multiple edges.[3]
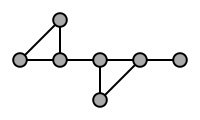
Example
In the following example, graph H is a minor of graph G:
The following diagram illustrates this. First construct a subgraph of G by deleting the dashed edges (and the resulting isolated vertex), and then contract the gray edge (merging the two vertices it connects):
Major results and conjectures
It is straightforward to verify that the Graph minor relation forms a partial order on the isomorphism classes of undirected graphs: it satisfies the transitive property (a minor of a minor of G is a minor of G itself), and G and H can only be minors of each other if they are isomorphic because any nontrivial minor operation removes edges. A deep result by Neil Robertson and Paul Seymour states that this partial order is actually a well-quasi-ordering: if an infinite list G1, G2,... of finite graphs is given, then there always exist two indices i < j such that Gi is a minor of Gj. Another equivalent way of stating this is that any set of graphs can have only a finite number of minimal elements under the minor ordering.[4] This result proved a conjecture formerly known as Wagner's conjecture, after Klaus Wagner; Wagner had conjectured it long earlier, but only published it in 1970.[5]
In the course of their proof, Seymour and Robertson also prove the graph structure theorem in which they determine, for any fixed graph H, the rough structure of any graph which does not have H as a minor. The statement of the theorem is itself long and involved, but in short it establishes that such a graph must have the structure of a clique-sum of smaller graphs that are modified in small ways from graphs embedded on surfaces of bounded genus. Thus, their theory establishes fundamental connections between graph minors and topological embeddings of graphs.[6]
For any graph H, the simple H-minor-free graphs must be sparse, which means that the number of edges is less than some constant multiple of the number of vertices.[7] More specifically, if H has h vertices, then a simple n-vertex simple H-minor-free graph can have at most
 edges, and some Kh-minor-free graphs have at least this many edges.[8] Additionally, the H-minor-free graphs have a separator theorem similar to the planar separator theorem for planar graphs: for any fixed H, and any n-vertex H-minor-free graph G, it is possible to find a subset of O(√n) vertices the removal of which splits G into two (possibly disconnected) subgraphs with at most 2n/3 vertices per subgraph.[9]
edges, and some Kh-minor-free graphs have at least this many edges.[8] Additionally, the H-minor-free graphs have a separator theorem similar to the planar separator theorem for planar graphs: for any fixed H, and any n-vertex H-minor-free graph G, it is possible to find a subset of O(√n) vertices the removal of which splits G into two (possibly disconnected) subgraphs with at most 2n/3 vertices per subgraph.[9]The Hadwiger conjecture in graph theory proposes that if a graph G does not contain a minor isomorphic to the complete graph on k vertices, then G has a proper coloring with k − 1 colors.[10] The case k = 5 is a restatement of the four color theorem. The Hadwiger conjecture has been proven only for k ≤ 6,[11] but remains unproven in the general case. Bollobás, Catlin & Erdős (1980) call it “one of the deepest unsolved problems in graph theory.” Another result relating the four-color theorem to graph minors is the snark theorem announced by Robertson, Sanders, Seymour, and Thomas, a strengthening of the four-color theorem conjectured by W. T. Tutte and stating that any bridgeless 3-regular graph that requires four colors in an edge coloring must have the Petersen graph as a minor.[12][13]
Minor-closed graph families
Many families of graphs have the property that every minor of a graph in F is also in F; such a class is said to be minor-closed. For instance, in any planar graph, or any embedding of a graph on a fixed topological surface, neither the removal of edges nor the contraction of edges can increase the genus of the embedding; therefore, planar graphs and the graphs embeddable on any fixed surface form minor-closed families.
If F is a minor-closed family, then (because of the well-quasi-ordering property of minors) among the graphs that do not belong to F there is a finite set X of minor-minimal graphs. These graphs are forbidden minors for F: a graph belongs to F if and only if it does not contain as a minor any graph in X. That is, every minor-closed family F can be characterized as the family of X-minor-free graphs for some finite set X of forbidden minors.[2] The best-known example of a characterization of this type is Wagner's theorem characterizing the planar graphs as the graphs having neither K5 nor K3,3 as minors.[1]
In some cases, the properties of the graphs in a minor-closed family may be closely connected to the properties of their excluded minors. For example a minor-closed graph family F has bounded pathwidth if and only if its forbidden minors include a forest,[14] F has bounded cycle rank if and only if its forbidden minors include a disjoint union of path graphs, F has bounded treewidth if and only if its forbidden minors include a planar graph,[15] and F has bounded local treewidth (a functional relationship between diameter and treewidth) if and only if its forbidden minors include an apex graph (a graph that can be made planar by the removal of a single vertex).[16] If H can be drawn in the plane with only a single crossing (that is, it has crossing number one) then the H-minor-free graphs have a simplified structure theorem in which they are formed as clique-sums of planar graphs and graphs of bounded treewidth.[17] For instance, both K5 and K3,3 have crossing number one, and as Wagner showed the K5-free graphs are exactly the 3-clique-sums of planar graphs and the eight-vertex Wagner graph, while the K3,3-free graphs are exactly the 2-clique-sums of planar graphs and K5.[18]
See "Robertson-Seymour theorem" for a list of minor-closed graph families.
Topological minors
A graph H is called a topological minor of a graph G if a subdivision of H is isomorphic to a subgraph of G.[19] It is easy to see that every topological minor is also a minor. The converse however is not true in general, but holds for graph with maximum degree not greater than 3.[20]
The topological minor relation is not a well-quasi-ordering on the set of finite graphs and hence the result of Robertson and Seymour does not apply to topological minors. However it is straightforward to construct finite forbidden topological minor characterizations from finite forbidden minor characterizations by replacing every branch set with k outgoing edges by every tree on k leaves that has down degree at least two.
Algorithms
The problem of deciding whether a graph G contains H as a minor is NP-complete in general; for instance, if H is a cycle graph with the same number of vertices as G, then H is a minor of G if and only if G contains a Hamiltonian cycle. However, when G is part of the input but H is fixed, it can be solved in polynomial time. More specifically, the running time for testing whether H is a minor of G in this case is O(n3), where n is the number of vertices in G and the big O notation hides a constant that depends superexponentially on H.[21] Thus, by applying the polynomial time algorithm for testing whether a given graph contains any of the forbidden minors, it is possible to recognize the members of any minor-closed family in polynomial time. However, in order to apply this result constructively, it is necessary to know what the forbidden minors of the graph family are.[22]
Notes
- ^ a b Lovász (2006), p. 77; Wagner (1937a).
- ^ a b Lovász (2006), theorem 4, p. 78; Robertson & Seymour (2004).
- ^ Lovász (2006) is inconsistent about whether to allow self-loops and multiple adjacencies: he writes on p.76 that "parallel edges and loops are allowed" but on p.77 he states that "a graph is a forest if and only if it does not contain the triangle K3 as a minor", true only for simple graphs.
- ^ Diestel (2005), Chapter 12: Minors, Trees, and WQO; Robertson & Seymour (2004).
- ^ Lovász (2006), p. 76.
- ^ Lovász (2006), pp. 80–82; Robertson & Seymour (2003).
- ^ Mader (1967).
- ^ Kostochka (1982); Kostochka (1984); Thomason (1984); Thomason (2001).
- ^ Alon, Seymour & Thomas (1990); Plotkin, Rao & Smith (1994); Reed & Wood (2009).
- ^ Hadwiger (1943).
- ^ Robertson, Seymour & Thomas (1993).
- ^ Pegg, Ed, Jr. (2002), "Book Review: The Colossal Book of Mathematics", Notices of the American Mathematical Society 49 (9): 1084–1086, http://www.ams.org/notices/200209/rev-pegg.pdf
- ^ Thomas, Robin, Recent Excluded Minor Theorems for Graphs, p. 14, http://people.math.gatech.edu/~thomas/PAP/bcc.pdf
- ^ Robertson & Seymour (1983).
- ^ Lovász (2006), Theorem 9, p. 81; Robertson & Seymour (1986).
- ^ Eppstein (2000); Demaine & Hajiaghayi (2004).
- ^ Robertson & Seymour (1993); Demaine, Hajiaghayi & Thilikos (2002).
- ^ Wagner (1937a); Wagner (1937b); Hall (1943).
- ^ Diestel 2005, p. 20
- ^ Diestel 2005, p. 22
- ^ Robertson & Seymour (1995).
- ^ Fellows & Langston (1988).
References
- Alon, Noga; Seymour, Paul; Thomas, Robin (1990), "A separator theorem for nonplanar graphs", Journal of the American Mathematical Society 3 (4): 801–808, doi:10.2307/1990903, JSTOR 1990903, MR1065053, http://www.ams.org/journals/jams/1990-03-04/S0894-0347-1990-1065053-0/home.html.
- Bollobás, B.; Catlin, P. A.; Erdős, Paul (1980), "Hadwiger's conjecture is true for almost every graph", European Journal on Combinatorics 1: 195–199, http://www2.renyi.hu/~p_erdos/1980-10.pdf.
- Demaine, Erik D.; Hajiaghayi, MohammadTaghi (2004), "Diameter and treewidth in minor-closed graph families, revisited", Algorithmica 40 (3): 211–215, doi:10.1007/s00453-004-1106-1, http://erikdemaine.org/papers/DiameterTreewidth_Algorithmica/.
- Demaine, Erik D.; Hajiaghayi, Mohammadtaghi; Thilikos, Dimitrios M. (2002), "1.5-Approximation for treewidth of graphs excluding a graph with one crossing as a minor", Proc. 5th International Workshop on Approximation Algorithms for Combinatorial Optimization (APPROX 2002), Lecture Notes in Computer Science, 2462, Springer-Verlag, pp. 67–80, doi:10.1007/3-540-45753-4_8
- Diestel, Reinhard (2005), Graph Theory (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-26183-4, http://www.math.uni-hamburg.de/home/diestel/books/graph.theory/.
- Eppstein, David (2000), "Diameter and treewidth in minor-closed graph families", Algorithmica 27: 275–291, doi:10.1007/s004530010020, MR2001c:05132.
- Fellows, Michael R.; Langston, Michael A. (1988), "Nonconstructive tools for proving polynomial-time decidability", Journal of the ACM 35 (3): 727–739, doi:10.1145/44483.44491.
- Hadwiger, Hugo (1943), "Über eine Klassifikation der Streckenkomplexe", Vierteljschr. Naturforsch. Ges. Zürich 88: 133–143.
- Hall, Dick Wick (1943), "A note on primitive skew curves", Bulletin of the American Mathematical Society 49 (12): 935–936, doi:10.1090/S0002-9904-1943-08065-2.
- Kostochka, A. V. (1982), "The minimum Hadwiger number for graphs with a given mean degree of vertices" (in Russian), Metody Diskret. Analiz. 38: 37–58.
- Kostochka, A. V. (1984), "Lower bound of the Hadwiger number of graphs by their average degree", Combinatorica 4: 307–316, doi:10.1007/BF02579141.
- Lovász, László (2006), "Graph minor theory", Bulletin of the American Mathematical Society 43 (1): 75–86, doi:10.1090/S0273-0979-05-01088-8.
- Mader, W. (1967), "Homomorphieeigenschaften und mittlere Kantendichte von Graphen", Mathematische Annalen 174 (4): 265–268, doi:10.1007/BF01364272.
- Plotkin, Serge; Rao, Satish; Smith, Warren D. (1994), "Shallow excluded minors and improved graph decompositions", Proc. 5th ACM–SIAM Symp. on Discrete Algorithms (SODA 1994), pp. 462–470, http://www.stanford.edu/~plotkin/lminors.ps.
- Reed, Bruce; Wood, David R. (2009), "A linear-time algorithm to find a separator in a graph excluding a minor", ACM Transactions on Algorithms 5 (4): Article 39, doi:10.1145/1597036.1597043.
- Robertson, Neil; Seymour, Paul (1983), "Graph minors. I. Excluding a forest", Journal of Combinatorial Theory, Series B 35 (1): 39–61, doi:10.1016/0095-8956(83)90079-5.
- Robertson, Neil; Seymour, Paul D. (1986), "Graph minors. V. Excluding a planar graph", Journal of Combinatorial Theory, Series B 41 (1): 92–114, doi:10.1016/0095-8956(86)90030-4
- Robertson, Neil; Seymour, Paul D. (1993), "Excluding a graph with one crossing", in Robertson, Neil; Seymour, Paul, Graph Structure Theory: Proc. AMS–IMS–SIAM Joint Summer Research Conference on Graph Minors, Contemporary Mathematics, 147, American Mathematical Society, pp. 669–675.
- Robertson, Neil; Seymour, Paul D. (1995), "Graph Minors. XIII. The disjoint paths problem", Journal of Combinatorial Theory, Series B 63 (1): 65–110, doi:10.1006/jctb.1995.1006.
- Robertson, Neil; Seymour, Paul D. (2003), "Graph Minors. XVI. Excluding a non-planar graph", Journal of Combinatorial Theory, Series B 89 (1): 43–76, doi:10.1016/S0095-8956(03)00042-X.
- Robertson, Neil; Seymour, Paul D. (2004), "Graph Minors. XX. Wagner's conjecture", Journal of Combinatorial Theory, Series B 92 (2): 325–357, doi:10.1016/j.jctb.2004.08.001.
- Robertson, Neil; Seymour, Paul; Thomas, Robin (1993), "Hadwiger's conjecture for K6-free graphs", Combinatorica 13: 279–361, doi:10.1007/BF01202354, http://www.math.gatech.edu/~thomas/PAP/hadwiger.pdf.
- Thomason, A. (1984), "An extremal function for contractions of graphs", Mathematical Proceedings of the Cambridge Philosophical Society 95 (2): 261–265, doi:10.1017/S0305004100061521.
- Thomason, A. (2001), "The extremal function for complete minors", Journal of Combinatorial Theory, Series B 81 (2): 318–338, doi:10.1006/jctb.2000.2013.
- Wagner, Klaus (1937a), "Über eine Eigenschaft der ebenen Komplexe", Math. Ann. 114: 570–590, doi:10.1007/BF01594196.
- Wagner, Klaus (1937b), "Über eine Erweiterung des Satzes von Kuratowski", Deutsche Mathematik 2: 280–285.
External links
- Weisstein, Eric W., "Graph Minor" from MathWorld.
Categories:- Graph minor theory
- Graph theory objects
Wikimedia Foundation. 2010.