- Moore graph
-
Unsolved problems in mathematics Does a Moore graph with girth 5 and degree 57 exist? 
In graph theory, a Moore graph is a regular graph of degree d and diameter k whose number of vertices equals the upper bound
An equivalent definition of a Moore graph is that it is a graph of diameter k with girth 2k + 1. Moore graphs were named by Hoffman & Singleton (1960) after Edward F. Moore, who posed the question of describing and classifying these graphs.
As well as having the maximum possible number of vertices for a given combination of degree and diameter, Moore graphs have the minimum possible number of vertices for a regular graph with given degree and girth. That is, any Moore graph is a cage (Erdõs, Rényi & Sós 1966). The formula for the number of vertices in a Moore graph can be generalized to allow a definition of Moore graphs with even girth as well as odd girth, and again these graphs are cages.
Contents
Bounding vertices by degree and diameter
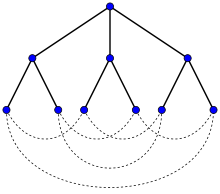 The Petersen graph as a Moore graph. Any breadth first search tree has d(d-1)i vertices in its ith level.
The Petersen graph as a Moore graph. Any breadth first search tree has d(d-1)i vertices in its ith level.
Let G be any graph with maximum degree d and diameter k, and consider the tree formed by breadth first search starting from any vertex v. This tree has 1 vertex at level 0 (v itself), and at most d vertices at level 1 (the neighbors of v). In the next level, there are at most d(d-1) vertices: each neighbor of v uses one of its adjacencies to connect to v and so can have at most d-1 neighbors at level 2. In general, a similar argument shows that at any level 1 ≤ i ≤ k, there can be at most d(d-1)i vertices. Thus, the total number of vertices can be at most
Hoffman & Singleton (1960) originally defined a Moore graph as a graph for which this bound on the number of vertices is met exactly. Therefore, any Moore graph has the maximum number of vertices possible among all graphs with maximum degree d and diameter k.
Later, Singleton (1968) showed that Moore graphs can equivalently be defined as having diameter k and girth 2k+1; these two requirements combine to force the graph to be d-regular for some d and to satisfy the vertex-counting formula.
Moore graphs as cages
Instead of upper bounding the number of vertices in a graph in terms of its maximum degree and its diameter, we can calculate via similar methods a lower bound on the number of vertices in terms of its minimum degree and its girth (Erdõs, Rényi & Sós 1966). Suppose G has minimum degree d and girth 2k+1. Choose arbitrarily a starting vertex v, and as before consider the breadth-first search tree rooted at v. This tree must have one vertex at level 0 (v itself), and at least d vertices at level 1. At level 2 (for k > 1), there must be at least d(d-1) vertices, because each vertex at level 1 has at least d-1 remaining adjacencies to fill, and no two vertices at level 1 can be adjacent to each other or to a shared vertex at level 2 because that would create a cycle shorter than the assumed girth. In general, a similar argument shows that at any level 1 ≤ i ≤ k, there must be at least d(d-1)i vertices. Thus, the total number of vertices must be at least
In a Moore graph, this bound on the number of vertices is met exactly. Each Moore graph has girth exactly 2k+1: it does not have enough vertices to have higher girth, and a shorter cycle would cause there to be too few vertices in the first k levels of some breadth first search tree. Therefore, any Moore graph has the minimum number of vertices possible among all graphs with minimum degree d and diameter k: it is a cage.
For even girth 2k, one can similarly form a breadth-first search tree starting from the midpoint of a single edge. The resulting bound on the minimum number of vertices in a graph of this girth with minimum degree d is
(The right hand side of the formula instead counts the number of vertices in a breadth first search tree starting from a single vertex, accounting for the possibility that a vertex in the last level of the tree may be adjacent to d vertices in the previous level.) Thus, the Moore graphs are sometimes defined as including the graphs that exactly meet this bound. Again, any such graph must be a cage.
Examples
Any odd cycle forms a Moore graph with degree 2, and any clique forms a Moore graph with diameter 1. The other known Moore graphs are:
- The Petersen graph with degree 3, diameter 2, and girth 5.
- The Hoffman–Singleton graph with degree 7, diameter 2, and girth 5.
The Hoffman–Singleton theorem states that any Moore graph with girth 5 must have degree 2, 3, 7, or 57. The graphs with degree 2, 3, and 7 are the pentagon, Petersen graph, and Hoffman–Singleton graph, respectively. It is not known whether a Moore graph with girth 5 and degree 57 exists, but Higman proved that it cannot be vertex-transitive, unlike the known ones.
If the generalized definition of Moore graphs that allows even girth graphs is used, the Moore graphs also include the complete bipartite graph Kn,n with girth four, the Heawood graph with degree 3 and girth 6, and the Tutte–Coxeter graph with degree 3 and girth 8. More generally, it is known (Bannai & Ito 1973; Damerell 1973) that, other than the graphs listed above, all Moore graphs must have girth 5, 6, 8, or 12.
See also
- The Degree diameter problem for graphs and digraphs
- Table of degree diameter graphs
References
- Bollobás, Béla (1998), "Chap.VIII.3", Modern graph theory, Graduate Texts in Mathematics, 184, Springer-Verlag.
- Bannai, E.; Ito, T. (1973), "On Moore graphs", J. Fac. Sci. Univ. Tokyo Ser. A 20: 191–208, MR0323615
- Damerell, R. M. (1973), "On Moore graphs", Proc. Cambridge Philos. Soc. 74: 227–236, doi:10.1017/S0305004100048015, MR0318004
- Erdõs, Paul; Rényi, Alfréd; Sós, Vera T. (1966), "On a problem of graph theory", Studia Sci. Math. Hungar. 1: 215–235, http://www.math-inst.hu/~p_erdos/1966-06.pdf.
- Hoffman, Alan J.; Singleton, Robert R. (1960), "Moore graphs with diameter 2 and 3", IBM Journal of Research and Development 5 (4): 497–504, MR0140437, http://www.research.ibm.com/journal/rd/045/ibmrd0405H.pdf
- Singleton, Robert R. (1968), "There is no irregular Moore graph", American Mathematical Monthly 75 (1): 42–43, doi:10.2307/2315106, MR0225679
External links
- Brouwer and Haemers: Spectra of graphs
- Weisstein, Eric W., "Moore Graph" from MathWorld.
- Weisstein, Eric W., "Hoffman-Singleton Theorem" from MathWorld.
Categories:- Graph families
- Regular graphs
Wikimedia Foundation. 2010.


