- Chiral anomaly
-
A chiral anomaly is the anomalous nonconservation of a chiral current. In some theories of fermions with chiral symmetry, the quantization may lead to the breaking of this (global) chiral symmetry. In that case, the charge associated with the chiral symmetry is not conserved.
The non-conservation happens in a tunneling process from one vacuum to another. Such a process is called an instanton. In the case of a symmetry related to the conservation of a fermionic particle number, one may understand the creation of such particles as follows. The definition of a particle is different in the two vacuum states between which the tunneling occurs; therefore a state of no particles in one vacuum corresponds to a state with some particles in the other vacuum.
In particular, there is a Dirac sea of fermions and, when such a tunneling happens, it causes the energy levels of the sea fermions to gradually shift upwards for the particles and downwards for the anti-particles, or vice versa. This means particles which once belonged to the Dirac sea become real (positive energy) particles and particle creation happens.
Technically, an anomalous symmetry is a symmetry of the action
 , but not of the measure
, but not of the measure  , and therefore not of the generating functional
, and therefore not of the generating functional  of the quantized theory (
of the quantized theory ( is Planck's action-quantum divided by 2π). The measure consists of a part depending of the fermion field
is Planck's action-quantum divided by 2π). The measure consists of a part depending of the fermion field  and a part depending on its complex conjugate
and a part depending on its complex conjugate  . The transformations of both parts under a chiral symmetry do not cancel in general. Note that if
. The transformations of both parts under a chiral symmetry do not cancel in general. Note that if  is a Dirac fermion, then the chiral symmetry can be written as
is a Dirac fermion, then the chiral symmetry can be written as  where
where  is some matrix acting on
is some matrix acting on  .
.From the formula for
 one also sees explicitly that in the classical limit,
one also sees explicitly that in the classical limit,  anomalies don't come into play, since in this limit only the extrema of
anomalies don't come into play, since in this limit only the extrema of  are relevant.
are relevant.The anomaly is in fact proportional to the instanton number of a gauge field to which the fermions are coupled (note that the gauge symmetry is always non-anomalous and is exactly respected, as is required by the consistency of the theory).
Contents
Calculation
The chiral anomaly can be calculated exactly by one-loop Feynman diagrams, e.g. the famous "triangle diagram", contributing to the pion decays,
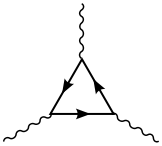 .
.Here, a wavy line signifies a photon, and the right-going (left-going) bold lines signify an electron and a positron, alternatingly. The fact that by encircling the triangle an odd number of times, a line which originally may be seen as a positron, returns as an electron, is actually already a signature for the anomalous behavior of the diagram.
This can also be calculated directly from the change in the measure of the fermionic fields under the chiral transformation.
Wess and Zumino developed a set of conditions on how the partition function ought to behave under gauge transformations called the Wess-Zumino consistency conditions.
Fujikawa derived this anomaly using the correspondence between functional determinants and the partition function using the Atiyah-Singer index theorem. See Fujikawa's method.
An example: baryonic charge non-conservation
The Standard Model of electroweak interactions has all the necessary ingredients for successful baryogenesis. Beyond the violation of charge conjugation C and CP violation CP (charge+parity), baryonic charge violation appears through the Adler-Bell-Jackiw anomaly of the U(1) group.
Baryons are not conserved by the usual electroweak interactions due to quantum chiral anomaly. The classic electroweak Lagrangian conserves baryonic charge. Quarks always enter in bilinear combinations
 , so that a quark can disappear only in collision with an antiquark. In other words, the classical baryonic current
, so that a quark can disappear only in collision with an antiquark. In other words, the classical baryonic current  is conserved:
is conserved:However, quantum corrections destroy this conservation law and instead of zero in the right hand side of this equation, one gets
where C is a numerical constant,
and the gauge field strength
 is given by the expression
is given by the expressionAn important fact is that the anomalous current non-conservation is proportional to the total derivative of a vector operator,
 (this is non-vanishing due to instanton configurations of the gauge field, which are pure gauge at the infinity), where the anomalous current Kμ is:
(this is non-vanishing due to instanton configurations of the gauge field, which are pure gauge at the infinity), where the anomalous current Kμ is:which is the Hodge dual of the Chern-Simons 3-form.
See also
- Anomaly (physics)
- Global anomaly
- Gravitational anomaly
- Strong CP problem
Further reading
Published articles
- S. Adler (1969). "Axial-Vector Vertex in Spinor Electrodynamics". Physical Review 177 (5): 2426. Bibcode 1969PhRv..177.2426A. doi:10.1103/PhysRev.177.2426.
- J.S. Bell and R. Jackiw (1969). "A PCAC puzzle: π0→γγ in the σ-model". Il Nuovo Cimento A 60: 47. Bibcode 1969NCimA..60...47B. doi:10.1007/BF02823296.
- P.H. Frampton and T.W. Kephart (1983). "Explicit Evaluation of Anomalies in Higher Dimensions". Physical Review Letters 50 (18): 1343. Bibcode 1983PhRvL..50.1343F. doi:10.1103/PhysRevLett.50.1343.
- P.H. Frampton and T.W. Kephart (1983). "Analysis of anomalies in higher space-time dimensions". Physical Review D28 (4): 1010. Bibcode 1983PhRvD..28.1010F. doi:10.1103/PhysRevD.28.1010.
- Alan R. White (2004). "Electroweak High-Energy Scattering and the Chiral Anomaly". Physical Review D69 (9): 096002. arXiv:hep-ph/0308287. Bibcode 2004PhRvD..69i6002W. doi:10.1103/PhysRevD.69.096002.
- T. Csörgő, R. Vértesi and J. Sziklai (2010). "Indirect Observation of an In-Medium η′ Mass Reduction in sqrt(s_{NN})=200 GeV Au+Au Collisions". Physical Review Letters 105: 182301. arXiv:0912.5526. Bibcode 2010PhRvL.105r2301C. doi:10.1103/PhysRevLett.105.182301.
Textbooks
- K. Fujikawa and H. Suzuki (May 2004). Path Integrals and Quantum Anomalies. Clarendon Press. ISBN 0-19-852913-9.
- S. Weinberg (2001). The Quantum Theory of Fields. Volume II: Modern Applications. Cambridge University Press. ISBN 0-521-55002-5.
Preprints
- Yang, J.-F. (2003). "Trace and chiral anomalies in QED and their underlying theory interpretation". arXiv:hep-ph/0309311 [hep-ph].
- Yang, J.-F. (2004). "Trace anomalies and chiral Ward identities". Chinese Physics Letters 21 (5): 792–794. arXiv:hep-ph/0403173. Bibcode 2004ChPhL..21..792Y. doi:10.1088/0256-307X/21/5/008.
- Gozzi, E.; Mauro, D.; Silvestri, A. (2004). "Chiral Anomalies via Classical and Quantum Functional Methods". International Journal of Modern Physics A [Particles and Fields; Gravitation; Cosmology; Nuclear Physics] 20 (20 & 21): 5009. arXiv:hep-th/0410129. Bibcode 2005IJMPA..20.5009G. doi:10.1142/S0217751X05025085.
- Dolgov, A.D. (1997). "Baryogenesis, 30 Years after". arXiv:hep-ph/9707419 [hep-ph].
Categories:- Anomalies in physics
- Quantum chromodynamics
- Standard Model
- Conservation laws
Wikimedia Foundation. 2010.





