- Edge contraction
-
In graph theory, an edge contraction is an operation which removes an edge from a graph while simultaneously merging together the two vertices it previously connected. Edge contraction is a fundamental operation in the theory of graph minors. Vertex identification is a less restrictive form of this operation.
Contents
Definition
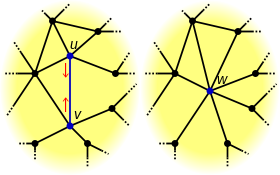
The edge contraction operation occurs relative to a particular edge, e. The edge e is removed and its two incident vertices, u and v, are merged into a new vertex w, where the edges incident to w each correspond to an edge incident to either u or v.
More generally, the operation may be performed on a set of edges by contracting each edge (in any order). Contractions may result in a graph with loops or multiple edges. These are sometimes deleted in order to keep within the class of simple graphs.
Formal definition
Let G=(V,E) be a graph (or directed graph) containing an edge e=(u,v) with u≠v. Let f be a function which maps every vertex in V\{u,v} to itself, and otherwise, maps it to a new vertex w. The contraction of e results in a new graph G′=(V′,E′), where V′=(V\{u,v})∪{w}, E′=E\{e}, and for every x∈V, x′=f(x)∈V′ is incident to an edge e′∈E′ if and only if, the corresponding edge, e∈E is incident to x in G.
Vertex identification
Vertex identification (sometimes called vertex contraction) removes the restriction that the contraction must occur over vertices sharing an incident edge. (Thus, edge contraction is a special case of vertex identification.) The operation may occur on any pair (or subset) of vertices in the graph. Edges between two contracting vertices are sometimes removed.
Path contraction
Path contraction occurs upon a the set of edges in a path that contract to form a single edge between the endpoints of the path. Edges incident to vertices along the path are either eliminated, or arbitrarily (or systematically) connected to one of the endpoints.
Applications
Both edge and vertex contraction techniques are valuable in proof by induction on the number of vertices or edges in a graph, where it can be assumed that a property holds for all smaller graphs and this can be used to prove the property for the larger graph.
Contractions are also useful in structures where we wish to simplify a graph by identifying vertices that represent essentially equivalent entities. One of the most common examples is the reduction of a general directed graph to an acyclic directed graph by contracting all of the vertices in each strongly connected component. If the relation described by the graph is transitive, no information is lost as long as we label each vertex with the set of labels of the vertices that were contracted to form it.
Another example is the coalescing performed in global graph coloring register allocation, where vertices are contracted (where it is safe) in order to eliminate move operations between distinct variables.
Edge contraction is used in 3D modelling packages (either manually, or through some feature of the modelling software) to consistently reduce vertex count, aiding in the creation of low-polygon models.
See also
- Subdivision (graph theory)
External links
Categories:
Wikimedia Foundation. 2010.