- Dynamic treatment regime
-
In medical research, a dynamic treatment regime (DTR) or adaptive treatment strategy is a set of rules for choosing effective treatments for individual patients. The treatment choices made for a particular patient are based on that individual's characteristics and history, with the goal of optimizing his or her long-term clinical outcome. A dynamic treatment regime is analogous to a policy in the field of reinforcement learning, and analogous to a controller in control theory. While most work on dynamic treatment regimes has been done in the context of medicine, the same ideas apply to time-varying policies in other fields, such as education, marketing, and economics.
Contents
History
Historically, medical research and the practice of medicine tended to rely on an acute care model for the treatment of all medical problems, including chronic illness (Wagner et al. 2001). More recently, the medical field has begun to look at long term care plans to treat patients with a chronic illness. This shift in ideology, coupled with increased demand for evidence based medicine and individualized care, has led to the application of sequential decision making research to medical problems and the formulation of dynamic treatment regimes.
Example
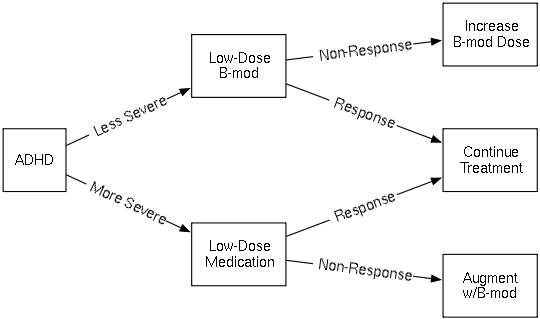
The figure below illustrates a hypothetical dynamic treatment regime for Attention Deficit Hyperactivity Disorder (ADHD). There are two decision points in this DTR. The initial treatment decision depends on the patient's baseline disease severity. The second treatment decision is a "responder/non-responder" decision: At some time after receiving the first treatment, the patient is assessed for response, i.e. whether or not the initial treatment has been effective. If so, that treatment is continued. If not, the patient receives a different treatment. In this example, for those who did not respond to initial medication, the second "treatment" is a package of treatments—it is the initial treatment plus behavior modification therapy. "Treatments" can be defined as whatever interventions are appropriate, whether they take the form of medications or other therapies.
Optimal Dynamic Treatment Regimes
The decisions of a dynamic treatment regime are made in the service of producing favorable clinical outcomes in patients who follow it. To make this more precise, the following mathematical framework is used:
Mathematical Formulation
For a series of decision time points,
 , define At to be the treatment ("action") chosen at time point t, and define Ot to be all clinical observations made at time t, immediately prior to treatment At. A dynamic treatment regime, π = (π1,...,πT) consists of a set of rules, one for each for each time point t, for choosing treatment At based clinical observations Ot. Thus πt(o1,a1,...,ot,at), is a function of the past and current observations, (o1,...,ot) and past treatments (a1,...,at − 1), which returns a choice of the current treatment, at.
, define At to be the treatment ("action") chosen at time point t, and define Ot to be all clinical observations made at time t, immediately prior to treatment At. A dynamic treatment regime, π = (π1,...,πT) consists of a set of rules, one for each for each time point t, for choosing treatment At based clinical observations Ot. Thus πt(o1,a1,...,ot,at), is a function of the past and current observations, (o1,...,ot) and past treatments (a1,...,at − 1), which returns a choice of the current treatment, at.Also observed at each time point is a measure of success called a reward Rt. The goal of a dynamic treatment regime is to make decisions that result in the largest possible expected sum of rewards, R = ∑ t R t. A dynamic treatment regime, π * is optimal if it satisfies
where E is an expectation over possible observations and rewards. The quantity E[R | treatments are chosen according to π] is often referred to as the value of π.
In the example above, the possible first treatments for A1 are "Low-Dose B-mod" and "Low-Dose Medication". The possible second treatments for A2 are "Increase B-mod Dose", "Continue Treatment", and "Augment w/B-mod". The observations O1 and O2 are the labels on the arrows: The possible O1 are "Less Severe" and "More Severe", and the possible O2 are "Non-Response" and "Response". The rewards R1,R2 are not shown; one reasonable possibility for reward would be to set R1 = 0 and set R2 to a measure of classroom performance after a fixed amount of time.
Delayed Effects
To find an optimal dynamic treatment regime, it might seem reasonable to find the optimal treatment that maximizes the immediate reward at each time point and then patch these treatment steps together to create a dynamic treatment regime. However, this approach is shortsighted and can result in an inferior dynamic treatment regime, because it ignores the potential for the current treatment action to influence the reward obtained at more distant time points.
For example a treatment may be desirable as a first treatment even if it does not achieve a high immediate reward. For example, when treating some kinds of cancer, a particular medication may not result in the best immediate reward (best acute effect) among initial treatments. However, this medication may impose sufficiently low side effects so that some non-responders are able to become responders with further treatment. Similarly a treatment that is less effective acutely may lead to better overall rewards, if it encourages/enables non-responders to adhere more closely to subsequent treatments.
Estimating Optimal Dynamic Treatment Regimes
Dynamic treatment regimes can be developed in the framework of evidence-based medicine, where clinical decision making is informed by data on how patients respond to different treatments. The data used to find optimal dynamic treatment regimes consist of the sequence of observations and treatments (o1,a1,o2,a2,..,oT,aT)i for multiple patients i = 1,...,n along with those patients' rewards Rt. A central difficulty is that intermediate outcomes both depend on previous treatments and determine subsequent treatment. However, if treatment assignment is independent of potential outcomes conditional on past observations—i.e., treatment is sequentially unconfounded—a number of algorithms exist to estimate the causal effect of time-varying treatments or dynamic treatment regimes.
While this type of data can be obtained through careful observation, it is often preferable to collect data through experimentation if possible. The use of experimental data, where treatments have been randomly assigned, is preferred because it helps eliminate bias caused by unobserved confounding variables that influence both the choice of the treatment and the clinical outcome. This is especially important when dealing with sequential treatments, since these biases can compound over time. Given an experimental data set, an optimal dynamic treatment regime can be estimated from the data using a number of different algorithms. Inference can also be done to determine whether the estimated optimal dynamic treatment regime results in significant improvements in expected reward over an alternative dynamic treatment regime.
Experimental design
Experimental designs of clinical trials that generate data for estimating optimal dynamic treatment regimes involve an initial randomization of patients to treatments, followed by re-randomizations at each subsequent time point to another treatment. The re-randomizations at each subsequent time point my depend on information collected after previous treatments, but prior to assigning the new treatment, such as how successful the previous treatment was. These types of trials were introduced and developed in Lavori & Dawson (2000), Lavori (2003) and Murphy (2005) and are often referred to as SMART trials (Sequential Multiple Assignment Randomized Trial). Some examples of SMART trials are the CATIE trial for treatment of Alzheimer's (Schneider et al. 2001) and the STAR*D trial for treatment of major depressive disorder (Lavori et al. 2001, Rush, Trivedi & Fava 2003).
SMART trials attempt to mimic the decision-making that occurs in clinical practice, but still retain the advantages of experimentation over observation. They can be more involved than single-stage randomized trials; however, they produce the data trajectories necessary for estimating optimal policies that take delayed effects into account. Several suggestions have been made to attempt to reduce complexity and resources needed. One can combine data over same treatment sequences within different treatment regimes. One may also wish to split up a large trial into screening, refining, and confirmatory trials (Collins et al. 2005). One can also use fractional factorial designs rather than a full factorial design (Nair et al. 2008), or target primary analyses to simple regime comparisons (Murphy 2005).
Reward construction
A critical part of finding the best dynamic treatment regime is the construction of a meaningful and comprehensive reward variable, Rt. To construct a useful reward, the goals of the treatment need to be well defined and quantifiable. The goals of the treatment can include multiple aspects of a patient's health and welfare, such as degree of symptoms, severity of side effects, time until treatment response, quality of life and cost. However, quantifying the various aspects of a successful treatment with a single function can be difficult, and work on providing useful decision making support that analyzes multiple outcomes is ongoing (Lizotte 2010). Ideally, the outcome variable should reflect how successful the treatment regime was in achieving the overall goals for each patient.
Variable selection and feature construction
Analysis is often improved by the collection of any variables that might be related to the illness or the treatment. This is especially important when data is collected by observation, to avoid bias in the analysis due to unmeasured confounders. Subsequently more observation variables are collected than are actually needed to estimate optimal dynamic treatment regimes. Thus variable selection is often required as a preprocessing step on the data before algorithms used to find the best dynamic treatment regime are employed.
Algorithms and Inference
Several algorithms exist for estimating optimal dynamic treatment regimes from data. Many of these algorithms were developed in the field of computer science to help robots and computers make optimal decisions in an interactive environment. These types of algorithms are often referred to as reinforcement learning methods (Sutton & Barto 1998) . The most popular of these methods used to estimate dynamic treatment regimes is called q-learning (Watkins 1989). In q-learning models are fit sequentially to estimate the value of the treatment regime used to collect the data and then the models are optimized with respect to the treatmens to find the best dynamic treatment regime. Many variations of this algorithm exist including modeling only portions of the Value of the treatment regime (Murphy 2003, Robins 2004). Using model-based Bayesian methods, the optimal treatment regime can also be calculated directly from posterior predictive inferences on the effect of dynamic policies (Zajonc 2010).
See also
References
- Banerjee, A.; Tsiatis, A. A. (2006), "Adaptive two-stage designs in phase II clinical trials", Statistics in Medicine 25 (19): 3382–3395
- Collins, L. M.; Murphy, S. A.; Nair, V.; Strecher, V. (2005), "A strategy for optimizing and evaluating behavioral interventions", Annals of Behavioral Medicine 30: 65–73
- Guo, X.; Tsiatis, A. A. (2005), "Estimation of survival distributions in two-stage randomization designs with censored data", International Journal of Biostatistics 1 (1)
- Hernán, Miguel A.; Lanoy, Emilie; Costagliola, Dominique; Robins, James M. (2006), "Comparison of Dynamic Treatment Regimes via Inverse Probability Weighting", Basic & Clinical Pharmacology & Toxicology 98: 237–242
- Lavori, P. W.; Dawson, R. (2000), "A design for testing clinical strategies: biased adaptive within-subject randomization", Journal of the Royal Statistical Society, Series A 163: 29–38
- Lavori, P.W.; Rush, A.J.; Wisniewski,, S.R.; Alpert, J.; Fava, M.; Kupfer, D.J.; Nierenberg, A.; Quitkin, F.M. et al. (2001), "Strengthening clinical effectiveness trials: Equipoise-stratified randomization", Biological Psychiatry 50: 792–801
- Lavori, P. W. (2003), "Dynamic treatment regimes: practical design considerations", Clinical Trials 1: 9–20
- Lizotte, D. L.; Bowling, M.; Murphy, S. A. (2010), "Efficient Reinforcement Learning with Multiple Reward Functions for Randomized Clinical Trial Analysis", Twenty-Seventh Annual International Conference on Machine Learning
- Lokhnygina, Y; Tsiatis, A. A. (2008), "Optimal two-stage group sequential designs", Journal of Statistical Planning and Inference 138: 489–499
- Lunceford, J. K.; Davidian, M.; Tsiatis, A. A. (2002), "Estimation of survival distributions of treatment policies in two-stage randomization designs in clinical trials", Biometrics 58: 48–57
- Moodie, E. E. M.; Richardson, T. S.; Stephens, D. A. (2007), "Demystifying optimal dynamic treatment regimes", Biometrics 63: 447–455
- Murphy, Susan A.; van der Laan, M. J.; Robins; CPPRG; (2001), "Marginal Mean Models for Dynamic Regimes", Journal of the American Statistical Association 96: 1410–1423
- Murphy, Susan A. (2003), "Optimal Dynamic Treatment Regimes", Journal of the Royal Statistical Society, Series B 65 (2): 331–366
- Murphy, Susan A. (2005), "An Experimental Design for the Development of Adaptive Treatment Strategies", Statistics in Medicine 24: 1455–1481
- Murphy, Susan A.; Daniel Almiral; (2008), "Dynamic Treatment Regimes", Encyclopedia of Medical Decision Making: #–#
- Nair, V.; Strecher, V.; Fagerlin, A.; Ubel, P.; Resnicow, K.; Murphy, S.; Little, R.; Chakraborty, B. et al. (2008), "Screening Experiments and Fractional Factorial Designs in Behavioral Intervention Research", The American Journal of Public Health 98 (8): 1534–1539
- Orellana, Liliana; Rotnitzky, Andrea; Robins, James M. (2010), "Dynamic Regime Marginal Structural Mean Models for Estimation of Optimal Dynamic Treatment Regimes, Part I: Main Content", The International Journal of Biostatistics 6 (2), http://www.bepress.com/ijb/vol6/iss2/8
- Orellana, Liliana; Rotnitzky, Andrea; Robins, James M. (2010), "Dynamic Regime Marginal Structural Mean Models for Estimation of Optimal Dynamic Treatment Regimes, Part II: Proofs of Results", The International Journal of Biostatistics 6 (2), http://www.bepress.com/ijb/vol6/iss2/9
- Robins, James M. (2004), "Optimal structural nested models for optimal sequential decisions", in Lin, D. Y.; Heagerty, P. J., Proceedings of the Second Seattle Symposium on Biostatistics, Springer, New York, pp. 189–326
- Robins, James M. (1986), "A new approach to causal inference in mortality studies with sustained exposure periods-application to control of the healthy worker survivor effect", Computers and Mathematics with Applications 14: 1393–1512
- Robins, James M. (1987), "Addendum to 'A new approach to causal inference in mortality studies with sustained exposure periods-application to control of the healthy worker survivor effect'", Computers and Mathematics with Applications 14: 923–945
- Rush, A.J.; Trivedi, M.; Fava (2003), "Depression IV: STAR*D treatment trial for depression", American Journal of Psychiatry 160 (2): 237
- Schneider, L.S.; Tariot, P.N.; Lyketsos, C.G.; Dagerman, K.S.; Davis, K.L.; Davis, S.; Hsiao, J.K.; Jeste, D.V. et al. (2001), "National Institute of Mental Health clinical antipsychotic trials of intervention effectiveness (CATIE) Alzheimer disease trial methodology", American Journal of Geriatric Psychiatry 9 (4): 346–360
- Sutton, R. S.; Barto, A. G. (1998), Reinforcement Learning: An Introduction, MIT Press, ISBN 0-262-19398-1, http://www.cs.ualberta.ca/~sutton/book/ebook/the-book.html
- van der Laan, M. J.; Robins, James M. (2003), Unified Methods for Censored Longitudinal Data and Causality, Springer-Verlag, ISBN 0-387-95556-9
- van der Laan, M. J.; Petersen, M. L. (2004), History-Adjusted Marginal Structural Models and Statically-Optimal Dynamic Treatment Regimes, http://works.bepress.com/mark_van_der_laan/83
- Wagner, E. H.; Austin, B. T.; Davis, C.; Hindmarsh, M.; Schaefer, J.; Bonomi, A. (2001), "Improving Chronic Illness Care: Translating Evidence Into Action", Health Affairs 20 (6): 64–78
- Wahed, A.. S.; Tsiatis, A. A. (2004), "Optimal estimator for the survival distribution and related quantities for treatment policies in two-stage randomization designs in clinical trials", Biometrics 60: 124–133
- Watkins, C. J. C. H. (1989), "Learning from Delayed Rewards", PhD thesis, Cambridge University, Cambridge, England
- Zhao, Y.; Kosorok, M. R.; Zeng, D. (2009), "Reinforcement learning design for cancer clinical trials", Statistics in Medicine 28: 3294–3315
Categories:
Wikimedia Foundation. 2010.

![\pi^* = \arg\max_{\pi}{E \big[R |\text{ treatments are chosen according to }\pi \big]} \!](c/85cebd3c93e506340e3db9a36e1f9e35.png)