- Dummy variable (statistics)
-
In statistics and econometrics, particularly in regression analysis, a dummy variable (also known as an indicator variable) is one that takes the values 0 or 1 to indicate the absence or presence of some categorical effect that may be expected to shift the outcome.[1] For example, in econometric time series analysis, dummy variables may be used to indicate the occurrence of wars, or major strikes. It could thus be thought of as a truth value represented as a numerical value 0 or 1 (as is sometimes done in computer programming).
Dummy variables are "proxy" variables or numeric stand-ins for qualitative facts in a regression model. In regression analysis, the dependent variables are influenced not only by quantitative variables (income, output, prices, etc.), but also by qualitative variables (gender, religion, geographic region, etc.) Dummy independent variables take the value of 0 or 1. Hence, they are also called binary variables. A dummy explanatory variable with a value of 0 will cause that variable's coefficient to disappear and a dummy with a value 1 will cause the coefficient to act as a supplemental intercept in a regression model. For example, suppose Gender is one of the qualitative variables relevant to a regression. Then, female and male would be the categories included under the Gender variable. If female is assigned the value of 1, then male would get the value 0 (or vice-versa).[2]
Thus, a dummy variable can be defined as a qualitative representative variable incorporated into a regression, such that it assumes the value 1 whenever the category it represents occurs, and 0 otherwise.[3] Dummy variables are used as devices to sort data into mutually exclusive categories (such as male/female, smoker/non-smoker, etc.).[4]
Dummy variables are generally used frequently in time series analysis with regime switching, seasonal analysis and qualitative data applications. Dummy variables are involved in studies for economic forecasting, bio-medical studies, credit scoring, response modelling, etc.. Dummy variables may be incorporated in traditional regression methods or newly developed modeling paradigms.[2]
Synonyms for the term dummy variables include design variables, Boolean indicators, proxies, indicator variables, categorical variables and qualitative variables.[2][4]
Contents
Incorporating a dummy independent variable
Dummy variables are incorporated in the same way as quantitative variables are included (as explanatory variables) in regression models. For example, if we consider a regression model of wage determination, wherein wages are dependent on gender (qualitative) and years of education (quantitative):
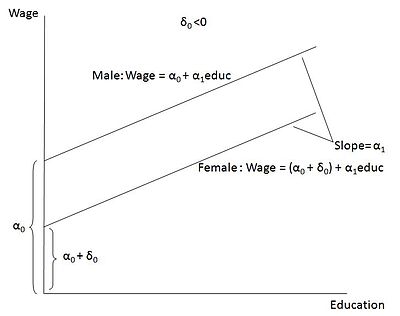
- Wage = α0 + δ0female + α1education + U
In the model, female = 1 when the person is a female and female = 0 when the person is male. δ0 can be interpreted as: the difference in wages between females and males, keeping education and the error term 'U' constant. Thus, δ0 helps to determine whether there is a discrimination in wages between men and women. If δ0<0 (negative coefficient), then for the same level of education (and other factors influencing wages), women earn a lower wage than men. On the other hand, if δ0>0 (positive coefficient), then women earn a higher wage than men (keeping other factors constant). Note that the coefficients attached to the dummy variables are called differential intercept coefficients. The model can be depicted graphically as an intercept shift between females and males. In the figure, the case δ0<0 is shown (wherein, men earn a higher wage than women).[5]
Dummy variables may be extended to more complex cases. For example, seasonal effects may be captured by creating dummy variables for each of the seasons: D1=1 if the observation is for summer, and equals zero otherwise; D2=1 if and only if autumn, otherwise equals zero; D3=1 if and only if winter, otherwise equals zero; and D4=1 if and only if spring, otherwise equals zero. In the panel data fixed effects estimator dummies are created for each of the units in cross-sectional data (e.g. firms or countries) or periods in a pooled time-series. However in such regressions either the constant term has to be removed, or one of the dummies removed making this the base category against which the others are assessed, for the following reason:
If dummy variables for all categories were included, their sum would equal 1 for all observations, which is identical to and hence perfectly correlated with the vector-of-ones variable whose coefficient is the constant term; if the vector-of-ones variable were also present, this would result in perfect multicollinearity,[6] so that the matrix inversion in the estimation algorithm would be impossible. This is referred to as the dummy variable trap.
ANOVA models
Main article: Analysis of varianceA regression model, in which all the explanatory variables are dummies or qualitative in nature, is called an Analysis of Variance (ANOVA) model. Here, the regressand will be quantitative and all the regressors will be exclusively qualitative in nature.[4]
ANOVA model with one qualitative variable
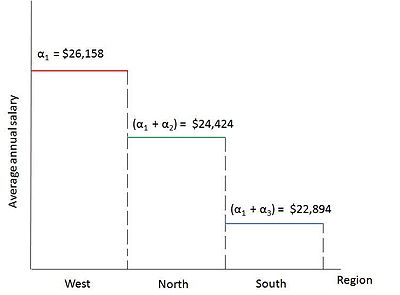
Suppose we want to run a regression to find out if the average annual salary of public school teachers differs among three geographical regions in Country A with 51 states: (1) North (21 states) (2) South (17 states) (3) West (13 states). Say that the simple arithmetic average salaries are as follows: $24,4214.14 (North), $22,894 (South), $26,158.62 (West). The arithmetic averages are different, but are they statistically different from each other? To compare the mean values,Analysis of Variance techniques can be used. The regression model can be defined as:
- Yi = α1 + α2D2i + α3D3i + Ui,
where
- Yi = average annual salary of public school teachers in state i
- D2i = 1 if the state i is in the North Region
- D2i = 0 otherwise (any region other than North)
- D3i = 1 if the state i is in the South Region
- D3i = 0 otherwise
In this model, we have only qualitative regressors, taking the value of 1 if the observation belongs to a specific category and 0 if it belongs to any other category. This makes it an ANOVA model.
Now, taking expectation of the model on both sides, we get,
Mean salary of public school teachers in the North Region:
E(Yi|D2i = 1, D3i = 0) = α1 + α2
Mean salary of public school teachers in the South Region:
E(Yi|D2i = 0 , D3i = 1) = α1 + α3
Mean salary of public school teachers in the West Region:
E(Yi|D2i = 0 , D3i = 0) = α1
(The error term does not get included in the expectation values as it is assumed that it satisfies the usual OLS conditions, i.e., E(Ui) = 0)
The expectation values can be interpreted as: The mean salary of public school teachers in the West is equal to the intercept term α1 in the multiple regression equation and the differential intercept coefficients, α2 and α3, explain by how much the mean salaries of teachers in the North and South Regions vary from that of the teachers in the West. Thus, the mean salaries of teachers in the North and South is compared against the mean salary of the teachers in the West. Hence, the West Region becomes the base group or the benchmark group,i.e., the group against which the comparisons are made. It is important to note that the omitted category, i.e., the category to which no dummy is assigned, is taken as the base group category.
Using the given data, the result of the regression would be:
- Ŷi = 26,158.62 − 1734.473D2i − 3264.615D3i
se = (1128.523) (1435.953) (1499.615)
t = (23.1759) (−1.2078) (−2.1776)
p = (0.0000) (0.2330) (0.0349)
R2 = 0.0901
where, se = standard error, t = t-statistics, p = p value
The regression result can be interpreted as: The mean salary of the teachers in the West (base group) is about $26,158, the salary of the teachers in the North is lower by about $1734 ($26,158.62 − $1734.473 = $24.424.14, which is the average salary of the teachers in the North) and that of the teachers in the South is lower by about $3265 ($26,158.62 − $3264.615 = $22,894, which is the average salary of the teachers in the South).
To find out if the mean salaries of the teachers in the North and South is statistically different from that of the teachers in the West (comparison category), we have to find out if the slope coefficients of the regression result are statistically significant. For this, we need to consider the p values. The estimated slope coefficient for the North is not statistically significant as its p value is 23 percent, however, that of the South is statistically significant as its p value is only around 3.5 percent. The overall result is that the mean salaries of the teachers in the West and North are statistically around the same but the mean salary of the teachers in the South is statistically lower by around $3265. The model is diagrammatically shown in Figure 2. This model is an ANOVA model with one qualitative variable having 3 categories.[4]
ANOVA model with two qualitative variables
Suppose we consider an ANOVA model having 2 qualitative variables, each with 2 categories: Hourly Wages in relation to Marital Status (Married / Unmarried)and Geographical Region (North / Non-North). Here, Marital Status and Geographical Region are the 2 explanatory dummy variables.[4]
Say the regression output on the basis of some given data appears as follows:
- Ŷi = 8.8148 + 1.0997D2 − 1.6729D3
where,
- Y = hourly wages (in $)
- D2 = marital status, 1 = married, 0 = otherwise
- D3 = geographical region, 1 = North, 0 = otherwise
In this model, a single dummy is assigned to each qualitative variable, and each variable has 2 categories included in it.
Here, the base group would become the omitted category: Unmarried, Non-North region (Unmarried people who do not live in the North region). All comparisons would be made in relation to this base group or omitted category. The mean hourly wage in the base category is about $8.81 (intercept term). In comparison, the mean hourly wage of those who are married is higher by about $1.10 and is equal to about $9.91 ($8.81 + $1.10). In contrast, the mean hourly wage of those who live in the North is lower by about $1.67 and is about $7.14 ($8.81 − $1.67).
Thus, if more than 1 qualitative variable is included in the regression, it is important to note that the omitted category should be chosen as the benchmark category and all comparisons will be made in relation to that category. The intercept term will show the expectation of the benchmark category and the slope coefficients will show by how much the other categories differ from the benchmark (omitted) category.[4]
ANCOVA models
Main article: Analysis of covarianceA regression model that contains a mixture of both quantitative as well as qualitative variables is called an Analysis of Covariance (ANCOVA) model. ANCOVA models are extensions of ANOVA models. They are capable of statistically controlling the effects of quantitative explanatory variables (also called covariates or control variables), in a model that involves quantitative as well as qualitative regressors.[4]
Now we will illustrate how qualitative and quantitative regressors are included to form ANCOVA models. Suppose we consider the same example used in the ANOVA model with 1 qualitative variable : average annual salary of public school teachers in 3 geographical regions of Country A. If we include a quantitative variable, State Government expenditure on public schools, to this regression, we get the following model:
- Yi = α1 + α2D2i + α3D3i + α4Xi + Ui
where,
- Yi = average annual salary of public school teachers in state i
- Xi = State expenditure on public schools per pupil
- D2i = 1, if the State i is in the North Region
- D2i = 0, otherwise
- D3i = 1, if the State i is in the South Region
- D3i = 0, otherwise
Say the regression output for this model looks like this:
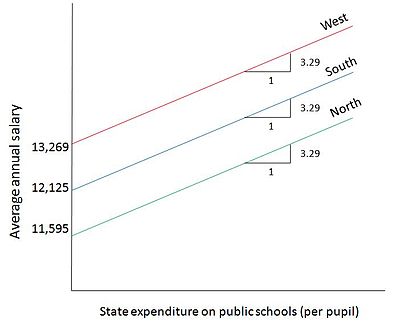
- Ŷi = 13,269.11 − 1673.514D2i − 1144.157D3i + 3.2889Xi
The result suggests that, for every $1 increase in State expenditure on public schools, a public school teacher's average salary goes up by about $3.29. Meanwhile, for a state in the North region, the mean salary of the teachers is lower than that of West region by about $1673 and for a state in the South region, the mean salary of teachers is lower than that of the West region by about $1144. This means that the mean salary of the teachers in the North is about $11,595 ($13,269.11 − $1673.514) and that of the teachers in the South is about $12,125 ($13,269.11 − $1144.157). The mean salary of the teachers in the West Region (omitted, base category) is about $13,269 (intercept term). Note that all these values have been obtained ceteris paribus. Figure 3 depicts this model diagrammatically. The average salary lines are parallel to each other as the slope is constant (keeping State expenditure constant for all 3 regions) and the trade off in the graph is between 2 quantitative variables: public school teacher's salary (Y) in relation to State expenditure on public schools (X).[4]
Interactions among dummy variables
Quantitative regressors in regression models often have an interaction among each other. In the same way qualitative regressors, or dummies, can also have interaction effects between each other and these interactions can be depicted in the regression model. For example,in a regression involving determination of wages, if 2 qualitative variables are considered, namely, gender and marital status,there could be an interaction between marital status and gender; in the sense that, there will be a difference in wages for female-married and female-unmarried.[5] These interactions can be shown in the regression equation as illustrated by the example below.
Suppose we consider the following regression, where Gender and Race are the 2 qualitative regressors and Years of education is the quantitative regressor:
- Yi = β1 + β2D2 + β3D3 + αXi + Ui
where,
- Y = Hourly Wages (in $)
- X = Years of education
- D2 = 1 if female, 0 otherwise
- D3 = 1 if non-white and non-Hispanic, 0 otherwise
There may be an interaction that occurs between the 2 qualitative variables, D2 and D3. For example, a female non-white / non-Hispanic may earn lower wages than a male non-white / non-Hispanic. The effect of the interacting dummies on the mean of Y may not be simply additive as in the case of the above examples, but multiplicative also, such as:
- Yi = β1 + β2D2 + β3D3 + β4(D2D3) + αXi + Ui
From this equation, we obtain:
Mean wages for female, non-white and non-Hispanic workers:
- E(Yi|D2 = 1, D3 = 1, Xi) = (β1 + β2 + β3 + β4) + αXi
Here,
- β2 = differential effect of being a female
- β3 = differential effect of being a non-white and non-Hispanic
- β4 = differential effect of being a female, non-white and non-Hispanic
The model shows that the mean wages of female non-white and non-Hispanic workers differs by β4 from the mean wages of females or non-white / non-Hispanics. Suppose all the 3 differential dummy coefficients are negative, it means that, female non-white and non-Hispanic workers earn much lower mean wages than female OR non-white and non-Hispanic workers as compared to the base group, which in this case is male, white or Hispanic (omitted category).
Thus, an interaction dummy (product of two dummies) can alter the dependent variable from the value that it gets when the two dummies are considered individually.[4]
Dummy dependent variables
What happens if the dependent variable is a dummy?
A dummy dependent variable model simply refers to a model in which the dependent variable, being influenced by the explanatory variables, is qualitative in nature. In other words, in such a regression, the dependent variable would be a dummy variable. Most decisions regarding 'how much' of an act must be performed involve a prior decision making on whether to perform the act or not. For example, amount of output to be produced, cost to be incurred, etc. involve prior decisions on to produce or not to produce, to spend or not to spend, etc. Such "prior decisions" become dependent dummies in the regression model.[7]
For example, the decision of a worker to be a part of the labour force becomes a dummy dependent variable. The decision is dichotomous, i.e., the decision would involve two actions: yes / no. If the worker decides to participate in the labour force, the decision would be 'yes', and it would be 'no' otherwise. So the dependent dummy would be Participation = 1 if participating, 0 if not participating. [4] Some other examples of dichotomous dependent dummies are cited below:
Decision: Choice of Occupation. Dependent Dummy: Supervisory = 1 if supervisor, 0 if not supervisor.
Decision: Affiliation to a Political Party. Dependent Dummy: Affiliation = 1 if affiliated to the party, 0 if not affiliated.
Decision: Retirement. Dependent Dummy: Retired = 1 if retired, 0 if not retired.
When the qualitative dependent dummy variable has more than 2 values (such as affiliation to many political parties), it becomes a multiresponse or a multinomial or polychotomous model.[7]
Dependent dummy variable models
Analysis of dependent dummy variable models can be done through different methods. One such method if the usual OLS method, which is called the Linear probability model, in case of a dependent dummy variable regression. This is the simplest procedure. Another alternative method is to say that there is an unobservable latent Y* variable, wherein, Y = 1 if Y* > 0, 0 otherwise. This is the underlying concept of the Logit and Probit models. It is important to note that all these models are for dichotomous dependent dummy variable regressions. These models are discussed in brief below.[8]
Linear probability model
Main article: Linear probability modelA regression model in which the dependent variable 'Y' is a dichotomous dummy, taking the values of 0 and 1, refers to a linear probability model (LPM).[8] Suppose we consider the following regression:
- Yi = α1 + α2Xi + Ui
where
- X = family income
- Y = 1 if a house is owned by the family, 0 if a house is not owned by the family
The model has been given the name linear probability model because, the regression is that of a linear one, and the conditional mean of Yi, when Xi is given [E(Yi|Xi)], refers to the conditional probability that the event will occur when Xi is given. This statement can be expressed as Pr(Yi = 1 |Xi). In this example, E(Yi|Xi)gives the probability of a house being owned by a family, whose income is given by Xi.
Now, using the OLS assumption, E(Ui) = 0, we get,
- E(Yi|Xi) = α1 + α2Xi
If Pi is probability that Yi occurs, i.e., Yi = 1, then (1 − Pi) is the probability that Yi does not occur, i.e., Yi = 0. Thus, the variable Yi has the Bernoulli probability distribution.
Expectation can now be defined as:
- E(Yi) = 0 (1 − Pi) + 1 (Pi) = Pi (from the probability distribution of Yi stated above)
From the above two expectation equations, we can get
- E(Yi|Xi) = α1 + α2Xi = Pi
This equation can be explained as: the conditional expectation of the regression model is the same as the conditional probability of the dependent Yi. Since probability lies between 0 and 1, it follows that
- 0 ≤ E(Yi|Xi) ≤ 1
i.e., the conditional expectation of the regression model lies between 0 and 1. This example illustrates how the OLS Method can be applied to the regression analysis of dependent dummy variable models.[4] However, some problems are inherent in the LPM model:
1. The regression line will not be a well-fitted one and hence measures of significance, such as R2, will not be reliable.
2. Models that are analyzed using the LPM approach will have heteroscedastic Variances of the disturbances.
3. The error-term will be a non-normal distribution as the Bernoulli distribution will be followed by it.
4. Probabilities must lie between 0 and 1. However, LPM may estimate values that are greater than 1 and less than 0. This will be difficult to interpret as the estimations are probabilities and probabilities greater than 1 or less than 0 do not exist.
5. There might exist a non-linear relationship between the variables of the LPM model, in which case, the linear regression will not fit the data accurately.[9][4]
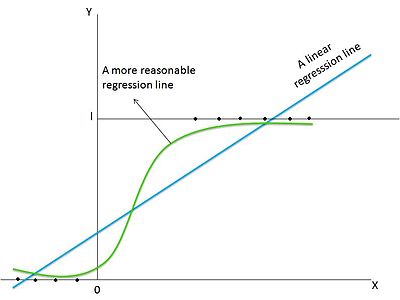
Figure 4 depicts the linear probability model graphically. The LPM analyzes a linear regression, wherein the graph would be a straight linear line, such as the blue line in the graph. However, in reality, the relationship among the variables is likely to be non-linear and hence, the green 'S'-shaped curve is a more appropriate regression line.[8]
Alternatives to LPM
After recognizing the limitations of the LPM, what was needed was a model that had the following features:
1. As the explanatory variable, Xi, increases, Pi = E (Y = 1 | X) must increase, but it should remain within the restriction, 0 ≤ E (Y = 1 | X) ≤ 1.
2. The relationship between the variables may be non-linear and hence, this non-linearity should be incorporated.
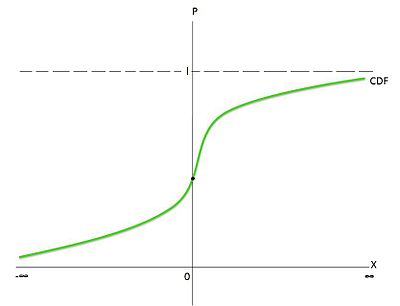
For this purpose, the cumulative distribution function (CDF) can be used to estimate the dependent dummy variable regression. Figure 5 shows an 'S'-shaped curve, which resembles the CDF of a random variable. In this model, the probability is between 0 and 1 and the non-linearity has been captured. The choice of the CDF to be used is now the question. All CDFs are 'S'-shaped, however, there is a unique CDF for each random variable.
The CDFs that have been chosen to represent the 0-1 models are the logistic and normal CDFs. The logistic CDFs gave rise to the logit model and the normal CDFs gave rise to the probit model.[4]
Logit model
Main article: Logistic regressionThe shortcomings of the LPM, led to the development of a more refined and improved model called the logit model. The logit model follows the Logistic CDF. This means that the cumulative distribution of the error term in the regression equation is logistic. [8]
The regression considered is non-linear, which presents the more realistic scenario of a non-linear relationship between the variables.
The logit model is estimated using the maximum likelihood approach. In this model, P(Y = 1 | X), which is the probability of the dependent variable taking the value of 1, given the independent variable is:
where zi = α1 + α2Xi
The model is then expressed in the form of the odds ratio, which gives the ratio between the probability of an event occurring and the probability of the event not occurring. Taking the natural log of the odds ratio, the logit (Li) is produced as:
This relationship shows that Li is linear in relation to Xi, but the probabilities are not linear. [9]
Probit model
Main article: Probit modelAnother Model that was developed to offset the disadvantages of the LPM was the Probit Model. The Probit Model follows the normal CDF. This means that the cumulative distribution of the error term in the regression equation is normal. [8]
The Probit Model is similar to the Logit Model with the same approach used. It used the normal CDF instead of the logistic CDF. The Probit model can be interpreted differently. McFadden has interpreted it using the utility theory or rational choice perspective on behaviour. In this model, an unobservable utility index Ii, which is also known as the latent variable is taken. This index is determined by the explanatory variables in the regression. Larger the value of the Index Ii, greater the probability of an event occurring. Using this, the Probit model has been constructed on the basis of the normal CDF.[9][4]
Precautions in the usage of dummy variables
1. If one dummy variable (that has been introduced as an explanatory variable) has n categories, it is important that only (n − 1) dummy variables are introduced. For example, if the dummy variable is gender, there are 2 categories (female / male). A dummy should be created only for one category, either female or male, and not both. The regression equation should incorporate that dummy along with the intercept term. If this rule is not complied with, the regression would lead to a dummy variable trap. A dummy variable trap is a situation where there is perfect collinearity or perfect multicollinearity between the variables, i.e., there would be an exact linear relationship among the variables. This can be explained as: The value of the intercept is implicitly given as 1 for every observation. Suppose the columns of all the n dummy categories under the qualititative variable are added up. This sum will produce exactly the intercept column as it is. This is the perfect collinearity situation that leads to the dummy variable trap. The way to avoid this is to introduce (n − 1) dummies + the intercept term OR to introduce n dummies and no intercept term. In both these cases there will be no linear relationship among the explanatory variables. However, the latter case is not recommended because it will make it difficult to test the dummy categories for differences from the base category. Hence, the (n − 1) dummies + intercept term approach is the most advised approach to form the regression model.[4][5]
2. The category for which the dummy is excluded or not assigned is known as the base group or the benchmark category. This category is the omitted category and all comparisons are made against this category. That is why it is also known as the comparison, reference or control category. This category should be carefully identified and omitted from the assignment of dummy variables.[4]
3. Since the base category does not have a dummy variable, the mean value of this category is equal to the intercept term itself. The value of this intercept term will thus be the value against which the categories having dummies should be compared.[4]
4. For comparison against the benchmark category, the "slope" coefficients of the dummy variables in the regression equation are considered. These "slope" coefficients are called differential intercept coefficients as they indicate by how much the mean value of the dummy categories differ from the mean value of the benchmark category (which is equal to the intercept).[4]
5. The choice of the benchmark category is completely at the discretion of the researcher. The researcher must take precaution to ensure that the intercept term is equal to the mean value of the benchmark category and all other dummy categories are compared against this benchmark category. [4]
See also
References
- ^ Draper, N.R.; Smith, H. (1998) Applied Regression Analysis, Wiley. ISBN 0-471-17082-8 (Chapter 14)
- ^ a b c , Asha Sharma, Susan Garavaglia. "A SMART GUIDE TO DUMMY VARIABLES: FOUR APPLICATIONS AND A MACRO". http://www.ats.ucla.edu/stat/sas/library/nesug98/p046.pdf.
- ^ "Interpreting the Coefficients on Dummy Variables". http://users.rcn.com/alancm/pp605/Interpreting_Dummy_Coefficients.pdf.
- ^ a b c d e f g h i j k l m n o p q r s Gujarati, Damodar N (2003). Basic econometrics. McGraw Hill. pp. 1002. ISBN 0072335424. http://www.mhhe.com/gujarati4e.
- ^ a b c Wooldridge, Jeffrey M (2009). Introductory econometrics: a modern approach. Cengage Learning. pp. 865. ISBN 0324581629. http://books.google.com/books?id=64vt5TDBNLwC&dq=introductory+econometrics+wooldridge&source=gbs_navlinks_s.
- ^ Suits, Daniel B. (1957). "Use of Dummy Variables in Regression Equations". Journal of the American Statistical Association 52 (280): 548–551. http://www.jstor.org/pss/2281705. Retrieved 2010-03-12.
- ^ a b Barreto, Humberto; Howland, Frank (2005). "Chapter 22: Dummy Dependent Variable Models". Introductory Econometrics: Using Monte Carlo Simulation with Microsoft Excel. Cambridge University Press. ISBN 0521843197. http://www3.wabash.edu/econometrics/EconometricsBook/chap22.htm.
- ^ a b c d e Maddala, G S (1992). Introduction to econometrics. Macmillan Pub. Co.. pp. 631. ISBN 0023745452. http://books.google.com/books?id=nBS3AAAAIAAJ&dq=introduction%20to%20econometrics%20maddala&source=gbs_book_other_versions.
- ^ a b c Adnan Kasman, "Dummy Dependent Variable Models". http://kisi.deu.edu.tr/evrim.gursoy/Dummy_Dependent_Variables_Models.doc.. Lecture Notes
External links
- http://www.stat.yale.edu/Courses/1997-98/101/anovareg.htm
- http://udel.edu/~mcdonald/statancova.html
- http://stat.ethz.ch/~maathuis/teaching/stat423/handouts/Chapter7.pdf
- http://socserv.mcmaster.ca/jfox/Courses/SPIDA/dummy-regression-notes.pdf
- http://hspm.sph.sc.edu/courses/J716/pdf/716-6%20Dummy%20Variables%20and%20Time%20Series.pdf
Categories:- Econometrics
- Regression analysis
- Statistical models
- Mathematical and quantitative methods (economics)
Wikimedia Foundation. 2010.