- Conic section
-
 Table of conics, Cyclopaedia, 1728
Table of conics, Cyclopaedia, 1728
In mathematics, a conic section (or just conic) is a curve obtained by intersecting a cone (more precisely, a right circular conical surface) with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2. It can be defined as the locus of points whose distances are in a fixed ratio to some point, called a focus, and some line, called a directrix.
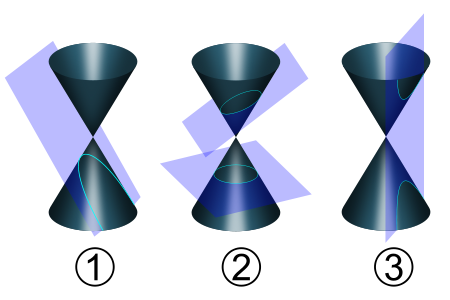
The three types of conic section are the hyperbola, the parabola, and the ellipse. The circle is a special case of the ellipse, and is of sufficient interest in its own right that it is sometimes called the fourth type of conic section.
The conic sections were named and studied as long ago as 200 BC, when Apollonius of Perga undertook a systematic study of their properties.
Contents
History
Menaechmus
It is believed that the first definition of a conic section is due to Menaechmus. This work does not survive, however, and is only known through secondary accounts. The definition used at that time differs from the one commonly used today in that it requires the plane cutting the cone to be perpendicular to one of the lines that generate the cone as a surface of revolution (a generatrix). Thus the shape of the conic is determined by the angle formed at the vertex of the cone (between two opposite generatrices): If the angle is acute then the conic is an ellipse; if the angle is right then the conic is a parabola; and if the angle is obtuse then the conic is a hyperbola. Note that the circle cannot be defined this way and was not considered a conic at this time.
Euclid is said to have written four books on conics but these were lost as well.[1] Archimedes is known to have studied conics, having determined the area bounded by a parabola and an ellipse. The only part of this work to survive is a book on the solids of revolution of conics.
Apollonius of Perga
The greatest progress in the study of conics by the ancient Greeks is due to Apollonius of Perga, whose eight volume Conic Sections summarized the existing knowledge at the time and greatly extended it. Apollonius's major innovation was to characterize a conic using properties within the plane and intrinsic to the curve; this greatly simplified analysis. With this tool, it was now possible to show that any plane cutting the cone, regardless of its angle, will produce a conic according to the earlier definition, leading to the definition commonly used today.
Pappus is credited with discovering importance of the concept of a focus of a conic, and the discovery of the related concept of a directrix.
Al-Kuhi
An instrument for drawing conic sections was first described in 1000 CE by the Islamic mathematician Al-Kuhi.[2][3]
Omar Khayyám
Apollonius's work was translated into Arabic (the technical language of the time) and much of his work only survives through the Arabic version. Persians found applications to the theory; the most notable of these was the Persian[4] mathematician and poet Omar Khayyám who used conic sections to solve algebraic equations.
Europe
Johannes Kepler extended the theory of conics through the "principle of continuity", a precursor to the concept of limits. Girard Desargues and Blaise Pascal developed a theory of conics using an early form of projective geometry and this helped to provide impetus for the study of this new field. In particular, Pascal discovered a theorem known as the hexagrammum mysticum from which many other properties of conics can be deduced. Meanwhile, René Descartes applied his newly discovered Analytic geometry to the study of conics. This had the effect of reducing the geometrical problems of conics to problems in algebra.
Features
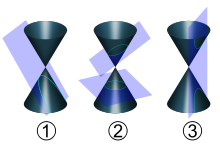
The three types of conics are the ellipse, parabola, and hyperbola. The circle can be considered as a fourth type (as it was by Apollonius) or as a kind of ellipse. The circle and the ellipse arise when the intersection of cone and plane is a closed curve. The circle is obtained when the cutting plane is parallel to the plane of the generating circle of the cone – for a right cone as in the picture at the top of the page this means that the cutting plane is perpendicular to the symmetry axis of the cone. If the cutting plane is parallel to exactly one generating line of the cone, then the conic is unbounded and is called a parabola. In the remaining case, the figure is a hyperbola. In this case, the plane will intersect both halves (nappes) of the cone, producing two separate unbounded curves.
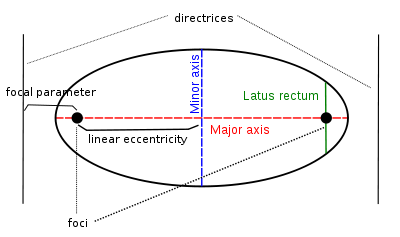
Various parameters are associated with a conic section, as shown in the following table. (For the ellipse, the table gives the case of a>b, for which the major axis is horizontal; for the reverse case, interchange the symbols a and b. For the hyperbola the east-west opening case is given. In all cases, a and b are positive.)
conic section equation eccentricity (e) linear eccentricity (c) semi-latus rectum (ℓ) focal parameter (p) circle 




ellipse 




parabola 




hyperbola 




Conic sections are exactly those curves that, for a point F, a line L not containing F and a non-negative number e, are the locus of points whose distance to F equals e times their distance to L. F is called the focus, L the directrix, and e the eccentricity.
The linear eccentricity (c) is the distance between the center and the focus (or one of the two foci).
The latus rectum (2ℓ) is the chord parallel to the directrix and passing through the focus (or one of the two foci).
The semi-latus rectum (ℓ) is half the latus rectum.
The focal parameter (p) is the distance from the focus (or one of the two foci) to the directrix.
The following relations hold:
Properties
Just as two (distinct) points determine a line, five points determine a conic. Formally, given any five points in the plane in general linear position, meaning no three collinear, there is a unique conic passing through them, which will be non-degenerate; this is true over both the affine plane and projective plane. Indeed, given any five points there is a conic passing through them, but if three of the points are collinear the conic will be degenerate (reducible, because it contains a line), and may not be unique; see further discussion.
Irreducible conic sections are always "smooth". More precisely, they never contain any inflection points. This is important for many applications, such as aerodynamics, where a smooth surface is required to ensure laminar flow and to prevent turbulence.
Intersection at infinity
An algebro-geometrically intrinsic form of this classification is by the intersection of the conic with the line at infinity, which gives further insight into their geometry:
- ellipses intersect the line at infinity in 0 points – rather, in 0 real points, but in 2 complex points, which are conjugate;
- parabolas intersect the line at infinity in 1 double point, corresponding to the axis – they are tangent to the line at infinity, and close at infinity, as distended ellipses;
- hyperbolas intersect the line at infinity in 2 points, corresponding to the asymptotes – hyperbolas pass through infinity, with a twist. Going to infinity along one branch passes through the point at infinity corresponding to the asymptote, then re-emerges on the other branch at the other side but with the inside of the hyperbola (the direction of curvature) on the other side – left vs. right (corresponding to the non-orientability of the real projective plane) – and then passing through the other point at infinity returns to the first branch. Hyperbolas can thus be seen as ellipses that have been pulled through infinity and re-emerged on the other side, flipped.
Degenerate cases
For more details on this topic, see Degenerate conic.There are five degenerate cases: three in which the plane passes through apex of the cone, and three that arise when the cone itself degenerates to a cylinder (a doubled line can occur in both cases).
When the plane passes through the apex, the resulting conic is always degenerate, and is either: a point (when the angle between the plane and the axis of the cone is larger than tangential); a straight line (when the plane is tangential to the surface of the cone); or a pair of intersecting lines (when the angle is smaller than the tangential). These correspond respectively to degeneration of an ellipse, parabola, and a hyperbola, which are characterized in the same way by angle. The straight line is more precisely a double line (a line with multiplicity 2) because the plane is tangent to the cone, and thus the intersection should be counted twice.
Where the cone is a cylinder, i.e. with the vertex at infinity, cylindric sections are obtained;[5] this corresponds to the apex being at infinity. Cylindrical sections are ellipses (or circles), unless the plane is vertical (which corresponds to passing through the apex at infinity), in which case three degenerate cases occur: two parallel lines, known as a ribbon (corresponding to an ellipse with one axis infinite and the other axis real and non-zero, the distance between the lines), a double line (an ellipse with one infinite axis and one axis zero), and no intersection (an ellipse with one infinite axis and the other axis imaginary).
Eccentricity, focus and directrix
The four defining conditions above can be combined into one condition that depends on a fixed point F (the focus), a line L (the directrix) not containing F and a nonnegative real number
 (the eccentricity). The corresponding conic section consists of the locus of all points whose distance to F equals
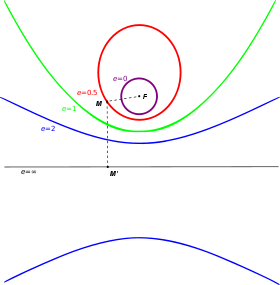
(the eccentricity). The corresponding conic section consists of the locus of all points whose distance to F equals  times their distance to L. For 0 < e < 1 we obtain an ellipse, for e = 1 a parabola, and for e > 1 a hyperbola.
times their distance to L. For 0 < e < 1 we obtain an ellipse, for e = 1 a parabola, and for e > 1 a hyperbola.For an ellipse and a hyperbola, two focus-directrix combinations can be taken, each giving the same full ellipse or hyperbola. The distance from the center to the directrix is a / e, where
 is the semi-major axis of the ellipse, or the distance from the center to the tops of the hyperbola. The distance from the center to a focus is
is the semi-major axis of the ellipse, or the distance from the center to the tops of the hyperbola. The distance from the center to a focus is  .
.In the case of a circle, the eccentricity e = 0, and one can imagine the directrix to be infinitely far removed from the center. However, the statement that the circle consists of all points whose distance to F is e times the distance to L is not useful, because we get zero times infinity.
The eccentricity of a conic section is thus a measure of how far it deviates from being circular.
For a given
 , the closer
, the closer  is to 1, the smaller is the semi-minor axis.
is to 1, the smaller is the semi-minor axis.Generalizations
Conics may be defined over other fields, and may also be classified in the projective plane rather than in the affine plane.
Over the complex numbers ellipses and hyperbolas are not distinct, since there is no meaningful difference between 1 and −1; precisely, the ellipse x2 + y2 = 1 becomes a hyperbola under the substitution y = iw, geometrically a complex rotation, yielding x2 − w2 = 1 – a hyperbola is simply an ellipse with an imaginary axis length. Thus there is a 2-way classification: ellipse/hyperbola and parabola. Geometrically, this corresponds to intersecting the line at infinity in either 2 distinct points (corresponding to two asymptotes) or in 1 double point (corresponding to the axis of a parabola), and thus the real hyperbola is a more suggestive image for the complex ellipse/hyperbola, as it also has 2 (real) intersections with the line at infinity.
In projective space, over any division ring, but in particular over either the real or complex numbers, all non-degenerate conics are equivalent, and thus in projective geometry one simply speaks of "a conic" without specifying a type, as type is not meaningful. Geometrically, the line at infinity is no longer special (distinguished), so while some conics intersect the line at infinity differently, this can be changed by a projective transformation – pulling an ellipse out to infinity or pushing a parabola off infinity to an ellipse or a hyperbola.
In other areas of mathematics
The classification into elliptic, parabolic, and hyperbolic is pervasive in mathematics, and often divides a field into sharply distinct subfields. The classification mostly arises due to the presence of a quadratic form (in two variables this corresponds to the associated discriminant), but can also correspond to eccentricity.
Quadratic form classifications:
- quadratic forms
- Quadratic forms over the reals are classified by Sylvester's law of inertia, namely by their positive index, zero index, and negative index: a quadratic form in n variables can be converted to a diagonal form, as
 where the number of +1 coefficients, k, is the positive index, the number of −1 coefficients, l, is the negative index, and the remaining variables are the zero index m, so k + l + m = n. In two variables the non-zero quadratic forms are classified as:
where the number of +1 coefficients, k, is the positive index, the number of −1 coefficients, l, is the negative index, and the remaining variables are the zero index m, so k + l + m = n. In two variables the non-zero quadratic forms are classified as:
- x2 + y2, – positive-definite (the negative is also included), corresponding to ellipses,
- x2 – degenerate, corresponding to parabolas, and
- x2 − y2 – indefinite, corresponding to hyperbolas.
- In two variables quadratic forms are classified by discriminant, analogously to conics, but in higher dimensions the more useful classification is as definite, (all positive or all negative), degenerate, (some zeros), or indefinite (mix of positive and negative but no zeros). This classification underlies many that follow.
- curvature
- The Gaussian curvature of a surface describes the infinitesimal geometry, and may at each point be either positive – elliptic geometry, zero – Euclidean geometry (flat, parabola), or negative – hyperbolic geometry; infinitesimally, to second order the surface looks like the graph of x2 + y2,, x2 (or 0), or x2 − y2.. Indeed, by the uniformization theorem every surface can be taken to be globally (at every point) positively curved, flat, or negatively curved. In higher dimensions the Riemann curvature tensor is a more complicated object, but manifolds with constant sectional curvature are interesting objects of study, and have strikingly different properties, as discussed at sectional curvature.
- Second order PDEs
- Partial differential equations (PDEs) of second order are classified at each point as elliptic, parabolic, or hyperbolic, accordingly as their second order terms correspond to an elliptic, parabolic, or hyperbolic quadratic form. The behavior and theory of these different types of PDEs are strikingly different – representative examples is that the Laplacian is elliptic, the heat equation is parabolic, and the wave equation is hyperbolic.
Eccentricity classifications include:
- Möbius transformations
- Real Möbius transformations (elements of PSL2(R) or its 2-fold cover, SL2(R)) are classified as elliptic, parabolic, or hyperbolic accordingly as their half-trace is

 or
or  mirroring the classification by eccentricity.
mirroring the classification by eccentricity. - Variance-to-mean ratio
- The variance-to-mean ratio classifies several important families of discrete probability distributions: the constant distribution as circular (eccentricity 0), binomial distributions as elliptical, Poisson distributions as parabolic, and negative binomial distributions as hyperbolic. This is elaborated at cumulants of some discrete probability distributions.
Cartesian coordinates
In the Cartesian coordinate system, the graph of a quadratic equation in two variables is always a conic section – though it may be degenerate, and all conic sections arise in this way. The equation will be of the form
As scaling all six constants yields the same locus of zeros, one can consider conics as points in the five-dimensional projective space

Discriminant classification
The conic sections described by this equation can be classified with the discriminant[6]
If the conic is non-degenerate, then:
- if B2 − 4AC < 0, the equation represents an ellipse;
- if A = C and B = 0, the equation represents a circle, which is a special case of an ellipse;
- if B2 − 4AC = 0, the equation represents a parabola;
- if B2 − 4AC > 0, the equation represents a hyperbola;
- if we also have A + C = 0, the equation represents a rectangular hyperbola.
To distinguish the degenerate cases from the non-degenerate cases, let ∆ be the determinant of the 3×3 matrix [A, B/2, D/2 ; B/2, C, E/2 ; D/2, E/2, F ]: that is, ∆ = (AC - B2/4)F + BED/4 - CD2/4 - AE2/4. Then the conic section is non-degenerate if and only if ∆ ≠ 0. If ∆=0 we have a point ellipse, two parallel lines (possibly coinciding with each other) in the case of a parabola, or two intersecting lines in the case of a hyperbola.[7]:p.63
Moreover, in the case of a non-degenerate ellipse (with B2 − 4AC < 0 and ∆≠0), we have a real ellipse if C∆ < 0 but an imaginary ellipse if C∆ > 0. An example is x2 + y2 + 10 = 0, which has no real-valued solutions.
Note that A and B are polynomial coefficients, not the lengths of semi-major/minor axis as defined in some sources.
Matrix notation
Main article: Matrix representation of conic sectionsThe above equation can be written in matrix notation as
The type of conic section is solely determined by the determinant of middle matrix: if it is positive, zero, or negative then the conic is an ellipse, parabola, or hyperbola respectively (see geometric meaning of a quadratic form). If both the eigenvalues of the middle matrix are non-zero (i.e. it is an ellipse or a hyperbola), we can do a transformation of variables to obtain

where a,c, and G satisfy
 and G = Aa2 + Cc2 + Bac − F.
and G = Aa2 + Cc2 + Bac − F.The quadratic can also be written as
If the determinant of this 3×3 matrix is non-zero, the conic section is not degenerate. If the determinant equals zero, the conic is a degenerate parabola (two parallel or coinciding lines), a degenerate ellipse (a point ellipse), or a degenerate hyperbola (two intersecting lines).
Note that in the centered equation with constant term G, G equals minus one times the ratio of the 3×3 determinant to the 2×2 determinant.
As slice of quadratic form
The equation
can be rearranged by taking the affine linear part to the other side, yielding
In this form, a conic section is realized exactly as the intersection of the graph of the quadratic form z = Ax2 + Bxy + Cy2 and the plane z = − (Dx + Ey + F). Parabolas and hyperbolas can be realized by a horizontal plane (D = E = 0), while ellipses require that the plane be slanted. Degenerate conics correspond to degenerate intersections, such as taking slices such as z = − 1 of a positive-definite form.
Eccentricity in terms of parameters of the quadratic form
When the conic section is written algebraically as
the eccentricity can be written as a function of the parameters of the quadratic equation.[8] If 4AC = B2 the conic is a parabola and its eccentricity equals 1 (if it is non-degenerate). Otherwise, assuming the equation represents either a non-degenerate hyperbola or a non-degenerate, non-imaginary ellipse, the eccentricity is given by
where η= 1 if the determinant of the 3×3 matrix is negative or η= -1 if that determinant is positive.
Standard form
Through change of coordinates these equations can be put in standard forms:
- Circle:

- Ellipse:

- Parabola:

- Hyperbola:

- Rectangular Hyperbola:

Such forms will be symmetrical about the x-axis and for the circle, ellipse and hyperbola symmetrical about the y-axis.
The rectangular hyperbola however is only symmetrical about the lines y = x and y = − x. Therefore its inverse function is exactly the same as its original function.These standard forms can be written as parametric equations,
- Circle: (acos θ,asin θ),
- Ellipse: (acos θ,bsin θ),
- Parabola: (at2,2at),
- Hyperbola: (asec θ,btan θ) or
 .
. - Rectangular hyperbola:

Invariants of conics
The trace and determinant of
 are both invariant with respect to both rotation of axes and translation of the plane (movement of the origin).[9]
are both invariant with respect to both rotation of axes and translation of the plane (movement of the origin).[9]The constant term F is invariant under rotation only.
Modified form
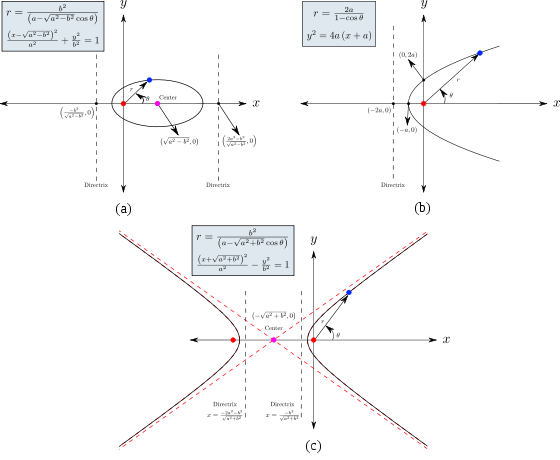
.
For some practical applications, it is important to re-arrange the standard form so that the focal-point can be placed at the origin. The mathematical formulation for a general conic section is then given in the polar form by
and in the Cartesian form by
From the above equation, the linear eccentricity (c) is given by
 .
.From the general equations given above, different conic sections can be represented as shown below:
- Circle:

- Ellipse:

- Parabola:

- Hyperbola:

Homogeneous coordinates
In homogeneous coordinates a conic section can be represented as:
- A1x2 + A2y2 + A3z2 + 2B1xy + 2B2xz + 2B3yz = 0.
Or in matrix notation
The matrix
 is called the matrix of the conic section.
is called the matrix of the conic section. is called the determinant of the conic section. If Δ = 0 then the conic section is said to be degenerate; this means that the conic section is either a union of two straight lines, a repeated line, a point or the empty set.
is called the determinant of the conic section. If Δ = 0 then the conic section is said to be degenerate; this means that the conic section is either a union of two straight lines, a repeated line, a point or the empty set.For example, the conic section
 reduces to the union of two lines:
reduces to the union of two lines:Similarly, a conic section sometimes reduces to a (single) repeated line:
 is called the discriminant of the conic section. If δ = 0 then the conic section is a parabola, if δ < 0, it is an hyperbola and if δ > 0, it is an ellipse. A conic section is a circle if δ > 0 and A1 = A2 and B1 = 0, it is an rectangular hyperbola if δ < 0 and A1 = −A2. It can be proven that in the complex projective plane CP2 two conic sections have four points in common (if one accounts for multiplicity), so there are never more than 4 intersection points and there is always one intersection point (possibilities: four distinct intersection points, two singular intersection points and one double intersection points, two double intersection points, one singular intersection point and 1 with multiplicity 3, 1 intersection point with multiplicity 4). If there exists at least one intersection point with multiplicity > 1, then the two conic sections are said to be tangent. If there is only one intersection point, which has multiplicity 4, the two conic sections are said to be osculating.[10]
is called the discriminant of the conic section. If δ = 0 then the conic section is a parabola, if δ < 0, it is an hyperbola and if δ > 0, it is an ellipse. A conic section is a circle if δ > 0 and A1 = A2 and B1 = 0, it is an rectangular hyperbola if δ < 0 and A1 = −A2. It can be proven that in the complex projective plane CP2 two conic sections have four points in common (if one accounts for multiplicity), so there are never more than 4 intersection points and there is always one intersection point (possibilities: four distinct intersection points, two singular intersection points and one double intersection points, two double intersection points, one singular intersection point and 1 with multiplicity 3, 1 intersection point with multiplicity 4). If there exists at least one intersection point with multiplicity > 1, then the two conic sections are said to be tangent. If there is only one intersection point, which has multiplicity 4, the two conic sections are said to be osculating.[10]Furthermore each straight line intersects each conic section twice. If the intersection point is double, the line is said to be tangent and it is called the tangent line. Because every straight line intersects a conic section twice, each conic section has two points at infinity (the intersection points with the line at infinity). If these points are real, the conic section must be a hyperbola, if they are imaginary conjugated, the conic section must be an ellipse, if the conic section has one double point at infinity it is a parabola. If the points at infinity are (1,i,0) and (1,-i,0), the conic section is a circle. If a conic section has one real and one imaginary point at infinity or it has two imaginary points that are not conjugated it is neither a parabola nor an ellipse nor a hyperbola.
Polar coordinates
In polar coordinates, a conic section with one focus at the origin and, if any, the other on the x-axis, is given by the equation
where e is the eccentricity and l is the semi-latus rectum (see below). As above, for e = 0, we have a circle, for 0 < e < 1 we obtain an ellipse, for e = 1 a parabola, and for e > 1 a hyperbola.
 Development of the conic section as the eccentricity e increases
Development of the conic section as the eccentricity e increases
Applications
The paraboloid shape of Archeocyathids produces conic sections on rock faces
Conic sections are important in astronomy: the orbits of two massive objects that interact according to Newton's law of universal gravitation are conic sections if their common center of mass is considered to be at rest. If they are bound together, they will both trace out ellipses; if they are moving apart, they will both follow parabolas or hyperbolas. See two-body problem.
In projective geometry, the conic sections in the projective plane are equivalent to each other up to projective transformations.
For specific applications of each type of conic section, see the articles circle, ellipse, parabola, and hyperbola.
For certain fossils in paleontology, understanding conic sections can help understand the three-dimensional shape of certain organisms.
Intersecting two conics
The solutions to a two second degree equations system in two variables may be seen as the coordinates of the intersections of two generic conic sections. In particular two conics may possess none, two or four possibly coincident intersection points. The best method of locating these solutions exploits the homogeneous matrix representation of conic sections, i.e. a 3x3 symmetric matrix which depends on six parameters.
The procedure to locate the intersection points follows these steps:
- given the two conics C1 and C2 consider the pencil of conics given by their linear combination λC1 + μC2
- identify the homogeneous parameters (λ,μ) which corresponds to the degenerate conic of the pencil. This can be done by imposing that det(λC1 + μC2) = 0, which turns out to be the solution to a third degree equation.
- given the degenerate conic C0, identify the two, possibly coincident, lines constituting it
- intersects each identified line with one of the two original conic; this step can be done efficiently using the dual conic representation of C0
- the points of intersection will represent the solution to the initial equation system
See also
- Focus (geometry), an overview of properties of conic sections related to the foci
- Lambert conformal conic projection
- Matrix representation of conic sections
- Quadrics, the higher-dimensional analogs of conics
- Quadratic function
- Rotation of axes
- Dandelin spheres
- Projective conics
- Elliptic coordinates
- Parabolic coordinates
- Director circle
Notes
- ^ Heath, T.L., The Thirteen Books of Euclid's Elements, Vol. I, Dover, 1956, pg.16
- ^ Stillwell, John (2010). Mathematics and its history (3rd ed. ed.). New York: Springer. p. 30. ISBN 144196052X.
- ^ "Apollonius of Perga Conics Books One to Seven". http://www.math.psu.edu/katok_s/Commentaries-new.pdf. Retrieved 10 June 2011.
- ^ Turner, Howard R. (1997). Science in medieval Islam: an illustrated introduction. University of Texas Press. p. 53. ISBN 0-292-78149-0. http://books.google.com/books?id=3VfY8PgmhDMC., Chapter , p. 53
- ^ "MathWorld: Cylindric section". http://mathworld.wolfram.com/CylindricSection.html.
- ^ Fanchi, John R. (2006), Math refresher for scientists and engineers, John Wiley and Sons, pp. 44–45, ISBN 0-471-75715-2, http://books.google.com/books?id=75mAJPcAWT8C, Section 3.2, page 45
- ^ Lawrence, J. Dennis, A Catalog of Special Plane Curves, Dover Publ., 1972.
- ^ Ayoub, Ayoub B., "The eccentricity of a conic section," The College Mathematics Journal 34(2), March 2003, 116-121.
- ^ Pettofrezzo, Anthony, Matrices and Transformations, Dover Publ., 1966, pp. 101-111.
- ^ Wilczynski, E. J. (1916), "Some remarks on the historical development and the future prospects of the differential geometry of plane curves", Bull. Amer. Math. Soc. 22: 317–329.
References
- Akopyan, A.V. and Zaslavsky, A.A. (2007). Geometry of Conics. American Mathematical Society. pp. 134. ISBN 0821843230.
External links
- Derivations of Conic Sections at Convergence
- Conic sections at Special plane curves.
- Weisstein, Eric W., "Conic Section" from MathWorld.
- Determinants and Conic Section Curves
- Occurrence of the conics. Conics in nature and elsewhere.
- Conics. An essay on conics and how they are generated.
- See Conic Sections at cut-the-knot for a sharp proof that any finite conic section is an ellipse and Xah Lee for a similar treatment of other conics.
- Cone-plane intersection MATLAB code
- Eight Point Conic at Dynamic Geometry Sketches
- An interactive Java conics grapher; uses a general second-order implicit equation.
Categories:- Conic sections
- Euclidean solid geometry
- Algebraic curves
- Birational geometry
- Analytic geometry
Wikimedia Foundation. 2010.