- Martin's maximum
-
In set theory, Martin's maximum, introduced by Foreman, Magidor & Shelah (1988), is a generalization of the proper forcing axiom, which is in turn a generalization of Martin's axiom.
Martin's maximum (MM) states that if D is a collection of
 dense subsets of a notion of forcing that preserves stationary subsets of ω1, then there is a D-generic filter. It is a well known fact that forcing with a ccc notion of forcing preserves stationary subsets of ω1, thus MM extends MA(
dense subsets of a notion of forcing that preserves stationary subsets of ω1, then there is a D-generic filter. It is a well known fact that forcing with a ccc notion of forcing preserves stationary subsets of ω1, thus MM extends MA( ). If (P,≤) is not a stationary set preserving notion of forcing, i.e., there is a stationary subset of ω1, which becomes nonstationary when forcing with (P,≤), then there is a collection D of
). If (P,≤) is not a stationary set preserving notion of forcing, i.e., there is a stationary subset of ω1, which becomes nonstationary when forcing with (P,≤), then there is a collection D of  dense subsets of (P,≤), such that there is no D-generic filter. This is why MM is called the maximal extension of Martin's axiom.
dense subsets of (P,≤), such that there is no D-generic filter. This is why MM is called the maximal extension of Martin's axiom.The existence of a supercompact cardinal implies the consistency of Martin's maximum. The proof uses Shelah's theories of semiproper forcing and iteration with revised countable supports.
MM implies that the value of the continuum is
 and that the ideal of nonstationary sets on ω1 is
and that the ideal of nonstationary sets on ω1 is  -saturated. It further implies stationary reflection, i.e., if S is a stationary subset of some regular cardinal κ≥ω2 and every element of S has countable cofinality, then there is an ordinal α<κ such that S∩α is stationary in α. In fact, S contains a closed subset of order type ω1.
-saturated. It further implies stationary reflection, i.e., if S is a stationary subset of some regular cardinal κ≥ω2 and every element of S has countable cofinality, then there is an ordinal α<κ such that S∩α is stationary in α. In fact, S contains a closed subset of order type ω1.References
- Foreman, M.; Magidor, M.; Shelah, S. (1988), "Martin's maximum, saturated ideals, and nonregular ultrafilters. I.", Ann. Of Math. (The Annals of Mathematics, Vol. 127, No. 1) 127 (1): 1–47, doi:10.2307/1971415, JSTOR 1971415, MR0924672 correction
- Jech, Thomas (2003), Set Theory: Millennium Edition, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-44085-7
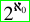
This set theory-related article is a stub. You can help Wikipedia by expanding it.
