Convex regular 4-polytope

The tesseract is one of 6 convex regular 4-polytopes

In mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids (in three dimensions) and the regular polygons (in two dimensions).

These polytopes were first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. Schläfli discovered that there are precisely six such figures. Five of these may be thought of as higher dimensional analogs of the Platonic solids. There is one additional figure (the 24-cell) which has no three-dimensional equivalent.

Each convex regular 4-polytope is bounded by a set of 3-dimensional cells which are all Platonic solids of the same type and size. These are fitted together along their respective faces in a regular fashion.

Properties

The following tables lists some properties of the six convex regular 4-dimensional polytopes. The symmetry groups of these polytopes are all Coxeter groups and given in the notation described in that article. The number following the name of the group is the order of the group.

Names	Family	Schläfli symbol	Vertices	Edges	Faces	Cells	Vertex figures	Dual polytope	Symmetry group
5-cell pentatope hyperpyramid hypertetrahedron 4-simplex	simplex (n-simplex)	{3,3,3}	5	10	10 triangles	5 tetrahedra	tetrahedra	(self-dual)	A4	120
8-cell Tesseract hypercube 4-cube	hypercube (n-cube)	{4,3,3}	16	32	24 squares	8 cubes	tetrahedra	16-cell	B4	384
16-cell orthoplex hyperoctahedron 4-orthoplex	cross-polytope (n-orthoplex)	{3,3,4}	8	24	32 triangles	16 tetrahedra	octahedra	tesseract	B4	384
24-cell octaplex polyoctahedron		{3,4,3}	24	96	96 triangles	24 octahedra	cubes	(self-dual)	F4	1152
120-cell dodecaplex hyperdodecahedron polydodecahedron		{5,3,3}	600	1200	720 pentagons	120 dodecahedra	tetrahedra	600-cell	H4	14400
600-cell tetraplex hypericosahedron polytetrahedron		{3,3,5}	120	720	1200 triangles	600 tetrahedra	icosahedra	120-cell	H4	14400

Since the boundaries of each of these figures is topologically equivalent to a 3-sphere, whose Euler characteristic is zero, we have the 4-dimensional analog of Euler's polyhedral formula:

$N_0 - N_1 + N_2 - N_3 = 0\,$

where N_k denotes the number of k-faces in the polytope (a vertex is a 0-face, an edge is a 1-face, etc.).

Visualizations

The following table shows some 2 dimensional projections of these polytopes. Various other visualizations can be found in the external links below. The Coxeter-Dynkin diagram graphs are also given below the Schläfli symbol.

5-cell	8-cell	16-cell	24-cell	120-cell	600-cell
{3,3,3}	{4,3,3}	{3,3,4}	{3,4,3}	{5,3,3}	{3,3,5}
Wireframe orthographic projections inside Petrie polygons.
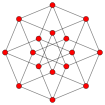
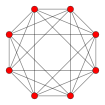
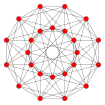
Solid orthographic projections
tetrahedral envelope (cell/vertex-centered)	cubic envelope (cell-centered)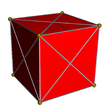	Cubic envelope (cell-centered)	cuboctahedral envelope (cell-centered)	truncated rhombic triacontahedron envelope (cell-centered)	Pentakis icosidodecahedral envelope (vertex-centered)
Wireframe Schlegel diagrams (Perspective projection)
(Cell-centered)	(Cell-centered)	(Cell-centered)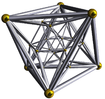	(Cell-centered)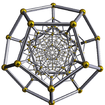	(Cell-centered)	(Vertex-centered)
Wireframe stereographic projections (Hyperspherical)

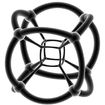
See also

• Infinite regular 4-polytopes:
  • One regular Euclidean honeycomb: {4,3,4}
  • Four regular hyperbolic honeycombs: {3,5,3}, {4,3,5}, {5,3,4}, {5,3,5}
• Nonconvex regular 4-polytopes:
  • Schläfli-Hess polychoron - Ten nonconvex regular 4-polytopes
• Abstract regular polychora:
  • 11-cell {3,5,3}
  • 57-cell {5,3,5}
• Uniform polychoron 4-polytope families constructed from the from these 6 regular forms.
• Regular polytope
• Platonic solid

References

• H. S. M. Coxeter, Introduction to Geometry, 2nd ed., John Wiley & Sons Inc., 1969. ISBN 0-471-50458-0.
• H. S. M. Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8.
• D. M. Y. Sommerville, An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, 1930. 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes

External links

• Weisstein, Eric W., "Regular polychoron" from MathWorld.
• Jonathan Bowers, 16 regular polychora
• Regular 4D Polytope Foldouts
• Catalog of Polytope Images A collection of stereographic projections of 4-polytopes.
• A Catalog of Uniform Polytopes
• Dimensions 2 hour film about the fourth dimension (contains stereographic projections of all regular polychorons)