- Tesseract
-
For other uses, see Tesseract (disambiguation).
Tesseract
8-cell
4-cube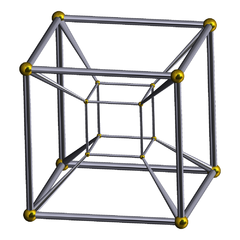
Schlegel diagramType Convex regular 4-polytope Schläfli symbol {4,3,3}
{4,3}x{}
{4}x{4}
{4}x{}x{}
{}x{}x{}x{}Coxeter-Dynkin diagram 


































Cells 8 (4.4.4) 
Faces 24 {4} Edges 32 Vertices 16 Vertex figure 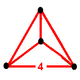
TetrahedronPetrie polygon octagon Coxeter group C4, [3,3,4] Dual 16-cell Properties convex, isogonal, isotoxal, isohedral Uniform index 10 In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8 cubical cells. The tesseract is one of the six convex regular 4-polytopes.
A generalization of the cube to dimensions greater than three is called a "hypercube", "n-cube" or "measure polytope". The tesseract is the four-dimensional hypercube, or 4-cube.
According to the Oxford English Dictionary, the word tesseract was coined and first used in 1888 by Charles Howard Hinton in his book A New Era of Thought, from the Greek τέσσερεις ακτίνες ("four rays"), referring to the four lines from each vertex to other vertices. Some people have called the same figure a tetracube, and also simply a hypercube (although the term hypercube is also used with dimensions greater than 4).
Contents
Geometry
The tesseract can be constructed in a number of ways. As a regular polytope with three cubes folded together around every edge, it has Schläfli symbol {4,3,3}. Constructed as a 4D hyperprism made of two parallel cubes, it can be named as a composite Schläfli symbol {4,3} × { }. As a duoprism, a Cartesian product of two squares, it can be named by a composite Schläfli symbol {4}×{4}.
Since each vertex of a tesseract is adjacent to four edges, the vertex figure of the tesseract is a regular tetrahedron. The dual polytope of the tesseract is called the hexadecachoron, or 16-cell, with Schläfli symbol {3,3,4}.
The standard tesseract in Euclidean 4-space is given as the convex hull of the points (±1, ±1, ±1, ±1). That is, it consists of the points:
A tesseract is bounded by eight hyperplanes (xi = ±1). Each pair of non-parallel hyperplanes intersects to form 24 square faces in a tesseract. Three cubes and three squares intersect at each edge. There are four cubes, six squares, and four edges meeting at every vertex. All in all, it consists of 8 cubes, 24 squares, 32 edges, and 16 vertices.
Projections to 2 dimensions
The construction of a hypercube can be imagined the following way:
- 1-dimensional: Two points A and B can be connected to a line, giving a new line segment AB.
- 2-dimensional: Two parallel line segments AB and CD can be connected to become a square, with the corners marked as ABCD.
- 3-dimensional: Two parallel squares ABCD and EFGH can be connected to become a cube, with the corners marked as ABCDEFGH.
- 4-dimensional: Two parallel cubes ABCDEFGH and IJKLMNOP can be connected to become a hypercube, with the corners marked as ABCDEFGHIJKLMNOP.
This structure is not easily imagined but it is possible to project tesseracts into three- or two-dimensional spaces. Furthermore, projections on the 2D-plane become more instructive by rearranging the positions of the projected vertices. In this fashion, one can obtain pictures that no longer reflect the spatial relationships within the tesseract, but which illustrate the connection structure of the vertices, such as in the following examples:
A tesseract is in principle obtained by combining two cubes. The scheme is similar to the construction of a cube from two squares: juxtapose two copies of the lower dimensional cube and connect the corresponding vertices. Each edge of a tesseract is of the same length. This view is of interest when using tesseracts as the basis for a network topology to link multiple processors in parallel computing: the distance between two nodes is at most 4 and there are many different paths to allow weight balancing.
Tesseracts are also bipartite graphs, just as a path, square, cube and tree are.
Parallel projections to 3 dimensions
 The rhombic dodecahedron forms the convex hull of the tesseracts vertex-first parallel-projection. The number of vertices in the layers of this projection is 1 4 6 4 1 - the fourth row in Pascal's triangle.
The rhombic dodecahedron forms the convex hull of the tesseracts vertex-first parallel-projection. The number of vertices in the layers of this projection is 1 4 6 4 1 - the fourth row in Pascal's triangle.
The cell-first parallel projection of the tesseract into 3-dimensional space has a cubical envelope. The nearest and farthest cells are projected onto the cube, and the remaining 6 cells are projected onto the 6 square faces of the cube.
The face-first parallel projection of the tesseract into 3-dimensional space has a cuboidal envelope. Two pairs of cells project to the upper and lower halves of this envelope, and the 4 remaining cells project to the side faces.
The edge-first parallel projection of the tesseract into 3-dimensional space has an envelope in the shape of a hexagonal prism. Six cells project onto rhombic prisms, which are laid out in the hexagonal prism in a way analogous to how the faces of the 3D cube project onto 6 rhombs in a hexagonal envelope under vertex-first projection. The two remaining cells project onto the prism bases.
The vertex-first parallel projection of the tesseract into 3-dimensional space has a rhombic dodecahedral envelope. There are exactly two ways of decomposing a rhombic dodecahedron into 4 congruent parallelepipeds, giving a total of 8 possible parallelepipeds. The images of the tesseract's cells under this projection are precisely these 8 parallelepipeds. This projection is also the one with maximal volume.
Image gallery
The tesseract can be unfolded into eight cubes into 3D space, just as the cube can be unfolded into six squares into 2D space (view animation). An unfolding of a polytope is called a net. There are 261 distinct nets of the tesseract.[1] The unfoldings of the tesseract can be counted by mapping the nets to paired trees (a tree together with a perfect matching in its complement).
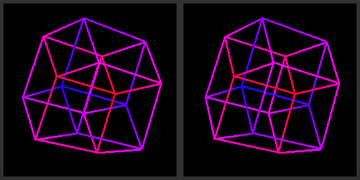
A stereoscopic 3D projection of a tesseract.Perspective projections

A 3D projection of an 8-cell performing a simple rotation about a plane which bisects the figure from front-left to back-right and top to bottom
A 3D projection of an 8-cell performing a double rotation about two orthogonal planes
Perspective with hidden volume elimination. The red corner is the nearest in 4D and has 4 cubical cells meeting around it.The tetrahedron forms the convex hull of the tesseract's vertex-centered central projection. Four of 8 cubic cells are shown. The 16th vertex is projected to infinity and the four edges to it are not shown.
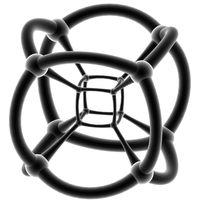
Stereographic projection
(Edges are projected onto the 3-sphere)
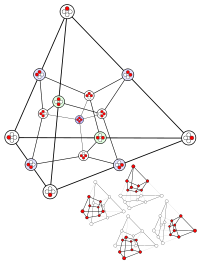
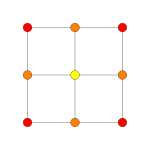
2D orthographic projections
orthographic projections Coxeter plane B4 B3 / D4 / A2 B2 / D3 Graph 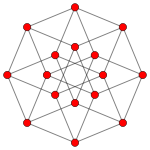
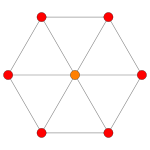
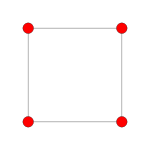
Dihedral symmetry [8] [6] [4] Coxeter plane F4 A3 Graph 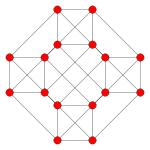
Dihedral symmetry [12/3] [4] Related uniform polytopes
Name tesseract rectified
tesseracttruncated
tesseractcantellated
tesseractruncinated
tesseractbitruncated
tesseractcantitruncated
tesseractruncitruncated
tesseractomnitruncated
tesseractCoxeter-Dynkin
diagram






























































Schläfli
symbol{4,3,3} t1{4,3,3} t0,1{4,3,3} t0,2{4,3,3} t0,3{4,3,3} t1,2{4,3,3} t0,1,2{4,3,3} t0,1,3{4,3,3} t0,1,2,3{4,3,3} Schlegel
diagram








B4 Coxeter plane graph 




Name 16-cell rectified
16-celltruncated
16-cellcantellated
16-cellruncinated
16-cellbitruncated
16-cellcantitruncated
16-cellruncitruncated
16-cellomnitruncated
16-cellCoxeter-Dynkin
diagram






























































Schläfli
symbol{3,3,4} t1{3,3,4} t0,1{3,3,4} t0,2{3,3,4} t0,3{3,3,4} t1,2{3,3,4} t0,1,2{3,3,4} t0,1,3{3,3,4} t0,1,2,3{3,3,4} Schlegel
diagram








B4 Coxeter plane graph 







See also
- Four-dimensional space
- 3-sphere
- Ludwig Schläfli - Polytopes
- Grande Arche - a monument and building in the business district of La Défense
- A Wrinkle in Time - a science fantasy novel using the word tesseract
Notes
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- H.S.M. Coxeter:
- Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
External links
- Weisstein, Eric W., "Tesseract" from MathWorld.
- Olshevsky, George, Tesseract at Glossary for Hyperspace.
- Richard Klitzing, 4D uniform polytopes (polychora), x4o3o3o - tes
- The Tesseract Ray traced images with hidden surface elimination. This site provides a good description of methods of visualizing 4D solids.
- Der 8-Zeller (8-cell) Marco Möller's Regular polytopes in R4 (German)
- WikiChoron: Tesseract
- HyperSolids is an open source program for the Apple Macintosh (Mac OS X and higher) which generates the five regular solids of three-dimensional space and the six regular hypersolids of four-dimensional space.
- Hypercube 98 via the Internet archive A Windows program that displays animated hypercubes, by Rudy Rucker
- ken perlin's home page A way to visualize hypercubes, by Ken Perlin
- Some Notes on the Fourth Dimension includes very good animated tutorials on several different aspects of the tesseract, by Davide P. Cervone
- Tesseract animation with hidden volume elimination
Fundamental convex regular and uniform polytopes in dimensions 2–10 Family An BCn Dn E6 / E7 / E8 / F4 / G2 Hn Regular polygon Triangle Square Hexagon Pentagon Uniform polyhedron Tetrahedron Octahedron • Cube Demicube Dodecahedron • Icosahedron Uniform polychoron 5-cell 16-cell • Tesseract Demitesseract 24-cell 120-cell • 600-cell Uniform 5-polytope 5-simplex 5-orthoplex • 5-cube 5-demicube Uniform 6-polytope 6-simplex 6-orthoplex • 6-cube 6-demicube 122 • 221 Uniform 7-polytope 7-simplex 7-orthoplex • 7-cube 7-demicube 132 • 231 • 321 Uniform 8-polytope 8-simplex 8-orthoplex • 8-cube 8-demicube 142 • 241 • 421 Uniform 9-polytope 9-simplex 9-orthoplex • 9-cube 9-demicube Uniform 10-polytope 10-simplex 10-orthoplex • 10-cube 10-demicube n-polytopes n-simplex n-orthoplex • n-cube n-demicube 1k2 • 2k1 • k21 pentagonal polytope Topics: Polytope families • Regular polytope • List of regular polytopes Categories:- Algebraic topology
- Four-dimensional geometry
- Polychora
Wikimedia Foundation. 2010.