Order-4 dodecahedral honeycomb

Order-4 dodecahedral honeycomb
Perspective projection view within Beltrami-Klein model
Type	Hyperbolic regular honeycomb
Schläfli symbol	{5,3,4} {5,31,1}
Coxeter-Dynkin diagram
Cells	dodecahedron {5,3}
Faces	pentagon {5}
Edge figure	square {4}
Vertex figure	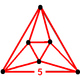octahedron
Cells/edge	{5,3}4
Cells/vertex	{5,3}8
Euler characteristic	0
Dual	Order-5 cubic honeycomb
Coxeter group	BH3, [5,3,4] DH3, [5,31,1]
Properties	Regular

In the geometry of hyperbolic 3-space, the order-4 dodecahedral honeycomb is one of four regular space-filling tessellation (or honeycombs). Four dodecahedra exist around each edge, and 8 dodecahedra around each vertex in an octahedral arrangement. Its vertices are constructed from 3 orthogonal axes. Its dual is the order-5 cubic honeycomb.

The dihedral angle of a dodecahedron is ~116.6°, so it is impossible to fit 4 of them on an edge in Euclidean 3-space. However in hyperbolic space a properly scaled dodecahedron can be scaled so that its dihedral angles are reduced to 90 degrees, and then four fit exactly on every edge.

Related polytopes and honeycombs

It is similar to the cubic honeycomb {4,3,4} of Euclidean 3-space. Both have an octahedral vertex figure, replacing the cubic cells by dodecahedra.

There are fifteen uniform honeycombs in the [5,3,4] Coxeter group family, including this regular form.

There are eleven uniform honeycombs in the bifurcating [5,3^1,1] Coxeter group family, including this honeycomb in its alternated form. This construction can be represented by alternation (checkerboard) with two colors of dodecahedral cells.

There is another regular honeycomb in hyperbolic 3-space called the order-5 dodecahedral honeycomb which has 5 dodecahedra per edge.

This honeycomb is also related to the 120-cell which has 120 dodecahedra in 4-dimensional space, with 3 dodecahedra on each edge.

See also

• Convex uniform honeycombs in hyperbolic space
• Poincaré homology sphere Poincaré dodecahedral space
• Seifert–Weber space Seifert–Weber dodecahedral space
• List of regular polytopes

References

• Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
• Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999 ISBN 0-486-40919-8 (Chapter 10: Regular honeycombs in hyperbolic space, Summary tables II,III,IV,V, p212-213)
• Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN 0-8247-0709-5 (Chapter 16-17: Geometries on Three-manifolds I,II) [1]

This Polychora article is a stub. You can help Wikipedia by expanding it.v · Categories: Honeycombs (geometry) Polychora stubs Wikimedia Foundation. 2010. Игры ⚽ Нужен реферат? List of Volkswagen Group diesel engines Live and Loud (Stiff Little Fingers) Look at other dictionaries: Order-5 dodecahedral honeycomb — (No image) Type Hyperbolic regular honeycomb Schläfli symbol {5,3,5} Coxeter Dynkin diagram …   Wikipedia Order-5 cubic honeycomb — Poincaré disk models Type Hyperbolic regular honeycomb Schläfli symbol …   Wikipedia Order-3 icosahedral honeycomb — The order 3 icosahedral honeycomb is one of four regular space filling tessellations (or honeycombs) in hyperbolic 3 space.Three icosahedra surround each edge, and 12 icosahedra surround each vertex, in a dodecahedral pattern.The dihedral angle… …   Wikipedia Honeycomb (geometry) — In geometry, a honeycomb is a space filling or close packing of polyhedral or higher dimensional cells , so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions. Honeycombs… …   Wikipedia Icosahedral honeycomb — Poincaré disk model Type regular hyperbolic honeycomb Schläfli symbol {3,5,3} Coxeter Dynkin diagram …   Wikipedia Convex uniform honeycombs in hyperbolic space — The {5,3,4} honeycomb in 3D hyperbolic space, viewed in perspective In geometry, a convex uniform honeycomb is a tessellation of convex uniform polyhedron cells. In 3 dimensional hyperbolic space there are nine Coxeter group f …   Wikipedia Nid d'abeille (géométrie) — Pour Nid d’abeille, voir Nid d abeille (homonymie). En géométrie, un nid d’abeille est le nom donné pour un pavage remplissant l’espace par des polyèdres, de la même manière qu’un pavage remplit un plan par des polygones. Le terme pavage est… …   Wikipédia en Français List of mathematics articles (O) — NOTOC O O minimal theory O Nan group O(n) Obelus Oberwolfach Prize Object of the mind Object theory Oblate spheroid Oblate spheroidal coordinates Oblique projection Oblique reflection Observability Observability Gramian Observable subgroup… …   Wikipedia 57-cell — In mathematics, the 57 cell (or pentacontaheptachoron) is a self dual abstract regular 4 polytope (four dimensional polytope). Its 57 cells are hemi dodecahedra. It also has 57 vertices, 171 edges and 171 faces. Its symmetry group is the… …   Wikipedia Seifert-Weber space — In mathematics, Seifert Weber space is a closed hyperbolic 3 manifold. It is also known as Seifert Weber dodecahedral space and hyperbolic dodecahedral space. It is one of the first discovered examples of closed hyperbolic 3 manifolds.To… …   Wikipedia 18+ © Academic, 2000-2024 Contact us: Technical Support, Advertising Dictionaries export, created on PHP, Joomla, Drupal, WordPress, MODx. Mark and share Search through all dictionaries Translate… Search Internet Share the article and excerpts Direct link … Do a right-click on the link above and select “Copy Link”