- Convex uniform honeycomb
-
 The alternated cubic honeycomb is one of 28 space-filling uniform tessellations in Euclidean 3-space, composed of alternating yellow tetrahedra and red octahedra.
The alternated cubic honeycomb is one of 28 space-filling uniform tessellations in Euclidean 3-space, composed of alternating yellow tetrahedra and red octahedra.
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.
Twenty-eight such honeycombs exist:
- the familiar cubic honeycomb and 7 truncations thereof;
- the alternated cubic honeycomb and 4 truncations thereof;
- 10 prismatic forms based on the uniform plane tilings (11 if including the cubic honeycomb);
- 5 modifications of some of the above by elongation and/or gyration.
They can be considered the three-dimensional analogue to the uniform tilings of the plane.
Contents
History
- 1900: Thorold Gosset enumerated the list of semiregular convex polytopes with regular cells (Platonic solids) in his publication On the Regular and Semi-Regular Figures in Space of n Dimensions, including one regular cubic honeycomb, and two semiregular forms with tetrahedra and octahedra.
- 1905: Alfredo Andreini enumerated 25 of these tessellations.
- 1991: Norman Johnson's manuscript Uniform Polytopes identified the complete list of 28.
- 1994: Branko Grünbaum, in his paper Uniform tilings of 3-space, also independently enumerated all 28, after discovering errors in Andreini's publication. He found the 1905 paper, which listed 25, had 1 wrong, and 4 being missing. Grünbaum states in this paper that Norman Johnson deserves priority for achieving the same enumeration in 1991. He also mentions that I. Alexeyev of Russia had contacted him regarding a putative enumeration of these forms, but that Grünbaum was unable to verify this at the time.
- 2006: George Olshevsky, in his manuscript Uniform Panoploid Tetracombs, along with repeating the derived list of 11 convex uniform tilings, and 28 convex uniform honeycombs, expands a further derived list of 143 convex uniform tetracombs (Honeycombs of uniform polychorons in 4-space).
Only 14 of the convex uniform polyhedra appear in these patterns:
- three of the five Platonic solids,
- six of the thirteen Archimedean solids, and
- five of the infinite family of prisms.
Names
This set can be called the regular and semiregular honeycombs. It has been called the Archimedean honeycombs by analogy with the convex uniform (non-regular) polyhedra, commonly called Archimedean solids. Recently Conway has suggested naming the set as the Architectonic tessellations and the dual honeycombs as the Catoptric tessellations.
The individual honeycombs are listed with names given to them by Norman Johnson. (Some of the terms used below are defined in Uniform polychoron#Geometric derivations.)
For cross-referencing, they are given with list indices from [A]ndreini (1-22), [W]illiams(1-2,9-19), [J]ohnson (11-19, 21-25, 31-34, 41-49, 51-52, 61-65), and [G]runbaum(1-28).
Compact Euclidean uniform tessellations (by their infinite Coxeter group families)
The fundamental infinite Coxeter groups for 3-space are:
- The
 , [4,3,4], cubic,
, [4,3,4], cubic, 





 (8 unique forms plus one alternation)
(8 unique forms plus one alternation) - The
 , [4,31,1], alternated cubic,
, [4,31,1], alternated cubic, 




 (11 forms, 3 new)
(11 forms, 3 new) - The
 cyclic group, [(3,3,3,3)],
cyclic group, [(3,3,3,3)], 

 (5 forms, one new)
(5 forms, one new)
In addition there are 5 special honeycombs which don't have pure reflectional symmetry and are constructed from reflectional forms with elongation and gyration operations.
The total unique honeycombs above are 18.
The prismatic stacks from infinite Coxeter groups for 3-space are:
- The
 x
x , [4,4]x[∞] prismatic group,
, [4,4]x[∞] prismatic group, 







 (2 new forms)
(2 new forms) - The
 x
x , [6,3]x[∞] prismatic group,
, [6,3]x[∞] prismatic group, 







 (7 unique forms)
(7 unique forms) - The
 x
x , (3 3 3)x[∞] prismatic group,
, (3 3 3)x[∞] prismatic group, 





 (No new forms)
(No new forms) - The
 x
x x
x , [∞]x[∞]x[∞] prismatic group,
, [∞]x[∞]x[∞] prismatic group, 









 (These all become a cubic honeycomb)
(These all become a cubic honeycomb)
In addition there is one special elongated form of the triangular prismatic honeycomb.
The total unique prismatic honeycombs above (excluding the cubic counted previously) are 10.
Combining these counts, 18 and 10 gives us the total 28 uniform honeycombs.
The C~3, [4,3,4] group (cubic)
The regular cubic honeycomb, represented by Schläfli symbol {4,3,4}, offers seven unique derived uniform honeycombs via truncation operations. (One redundant form, the runcinated cubic honeycomb, is included for completeness though identical to the cubic honeycomb.)
Reference
IndicesHoneycomb name
Coxeter-Dynkin
and Schläfli
symbolsCell counts/vertex
and positions in cubic honeycomb(0)





(1)





(2)





(3)





Solids
(Partial)Frames
(Perspective)Vertex figure J11,15
A1
W1
G22cubic







t0{4,3,4}(8)

(4.4.4)

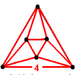
octahedronJ12,32
A15
W14
G7rectified cubic







t1{4,3,4}(2)

(3.3.3.3)(4)

(3.4.3.4)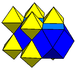

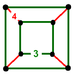
cuboidJ13
A14
W15
G8truncated cubic







t0,1{4,3,4}(1)

(3.3.3.3)(4)

(3.8.8)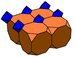

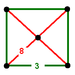
square pyramidJ14
A17
W12
G9cantellated cubic







t0,2{4,3,4}(1)

(3.4.3.4)(2)

(4.4.4)(2)

(3.4.4.4)

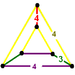
obilique triangular prismJ11,15 runcinated cubic
(same as regular cubic)







t0,3{4,3,4}(1)

(4.4.4)(3)

(4.4.4)(3)

(4.4.4)(1)

(4.4.4)

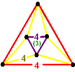
octahedronJ16
A3
W2
G28bitruncated cubic







t1,2{4,3,4}(2)

(4.6.6)(2)

(4.6.6)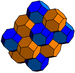

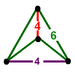
(disphenoid tetrahedron)J17
A18
W13
G25cantitruncated cubic







t0,1,2{4,3,4}(1)

(4.6.6)(1)

(4.4.4)(2)
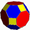
(4.6.8)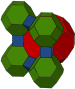

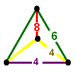
irregular tetrahedronJ18
A19
W19
G20runcitruncated cubic







t0,1,3{4,3,4}(1)

(3.4.4.4)(1)

(4.4.4)(2)

(4.4.8)(1)

(3.8.8)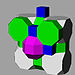

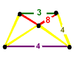
oblique trapezoidal pyramidJ19
A22
W18
G27omnitruncated cubic







t0,1,2,3{4,3,4}(1)

(4.6.8)(1)

(4.4.8)(1)

(4.4.8)(1)

(4.6.8)

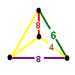
irregular tetrahedronJ21,31,51
A2
W9
G1alternated cubic







h0{4,3,4}(6)

(3.3.3.3)(8)

(3.3.3)


cuboctahedronB~4, [4,31,1] group
The
 group offers 11 derived forms via truncation operations, four being unique uniform honeycombs.
group offers 11 derived forms via truncation operations, four being unique uniform honeycombs.The honeycombs from this group are called alternated cubic because the first form can be seen as a cubic honeycomb with alternate vertices removed, reducing cubic cells to tetrahedra and creating octahedron cells in the gaps.
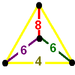
Nodes are indexed left to right as 0,1,0',3 with 0' being below and interchangeable with 0. The alternate cubic names given are based on this ordering.
Referenced
indicesHoneycomb name
Coxeter-Dynkin
diagramCells by location
(and count around each vertex)Solids
(Partial)Frames
(Perspective)vertex figure (0)




(1)





(0')





(3)



J21,31,51
A2
W9
G1alternated cubic





 (6)
(6)
(3.3.3.3) (8)
(8)
(3.3.3)


cuboctahedronJ22,34
A21
W17
G10truncated alternated cubic





 (1)
(1)
(3.4.3.4) (2)
(2)
(4.6.6) (2)
(2)
(3.6.6)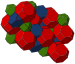

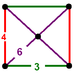
rectangular pyramidJ12,32
A15
W14
G7rectified cubic
(rectified alternate cubic)





 (2)
(2)
(3.4.3.4) (2)
(2)
(3.4.3.4) (2)
(2)
(3.3.3.3)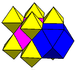

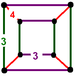
cuboidJ12,32
A15
W14
G7rectified cubic
(cantellated alternate cubic)





 (1)
(1)
(3.3.3.3) (1)
(1)
(3.3.3.3) (4)
(4)
(3.4.3.4)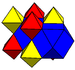

cuboidJ16
A3
W2
G28bitruncated cubic
(cantitruncated alternate cubic)





 (1)
(1)
(4.6.6) (1)
(1)
(4.6.6) (2)
(2)
(4.6.6)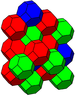

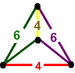
isosceles tetrahedronJ13
A14
W15
G8truncated cubic
(bicantellated alternate cubic)





 (2)
(2)
(3.8.8) (2)
(2)
(3.8.8) (1)
(1)
(3.3.3.3)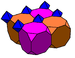

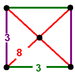
square pyramidJ11,15
A1
W1
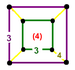
G22cubic
(trirectified alternate cubic)





 (4)
(4)
(4.4.4) (4)
(4)
(4.4.4)


octahedronJ23
A16
W11
G5runcinated alternated cubic





 (1)
(1)
cube (3)
(3)
(3.4.4.4) (1)
(1)
(3.3.3)

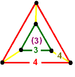
tapered triangular prismJ14
A17
W12
G9cantellated cubic
(runcicantellated alternate cubic)





 (1)
(1)
(3.4.4.4) (2)
(2)
(4.4.4) (1)
(1)
(3.4.4.4) (1)
(1)
(3.4.3.4)

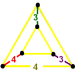
obilique triangular prismJ24
A20
W16
G21cantitruncated alternated cubic
(or runcitruncated alternate cubic)





 (1)
(1)
(3.8.8) (2)
(2)
(4.6.8) (1)
(1)
(3.6.6)

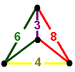
Irregular tetrahedronJ17
A18
W13
G25cantitruncated cubic
(omnitruncated alternated cubic)





 (1)
(1)
(4.6.8) (1)
(1)
(4.4.4) (1)
(1)
(4.6.8) (1)
(1)
(4.6.6)

irregular tetrahedronA~3, [(3,3,3,3)] group
There are 5 forms[1] constructed from the
 group, of which only the quarter cubic honeycomb is unique.
group, of which only the quarter cubic honeycomb is unique.Referenced
indicesHoneycomb name
Coxeter-Dynkin
diagramCells by location
(and count around each vertex)Solids
(Partial)Frames
(Perspective)vertex figure (0)



(1)



(2)



(3)



J21,31,51
A2
W9
G1alternated cubic



 (4)
(4)
(3.3.3) (6)
(6)
(3.3.3.3) (4)
(4)
(3.3.3)


cuboctahedronJ12,32
A15
W14
G7rectified cubic



 (2)
(2)
(3.4.3.4) (1)
(1)
(3.3.3.3) (2)
(2)
(3.4.3.4) (1)
(1)
(3.3.3.3)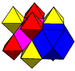

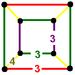
cuboidJ25,33
A13
W10
G6quarter cubic



 (1)
(1)
(3.3.3) (1)
(1)
(3.3.3) (3)
(3)
(3.6.6) (3)
(3)
(3.6.6)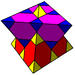

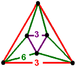
triangular antiprismJ22,34
A21
W17
G10truncated alternated cubic



 (1)
(1)
(3.6.6) (1)
(1)
(3.4.3.4) (1)
(1)
(3.6.6) (2)
(2)
(4.6.6)

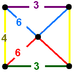
Rectangular pyramidJ16
A3
W2
G28bitruncated cubic



 (1)
(1)
(4.6.6) (1)
(1)
(4.6.6) (1)
(1)
(4.6.6) (1)
(1)
(4.6.6)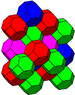

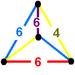
isosceles tetrahedronNonwythoffian forms (gyrated and elongated)
Three more uniform honeycombs are generated by breaking one or another of the above honeycombs where its faces form a continuous plane, then rotating alternate layers by 60 or 90 degrees (gyration) and/or inserting a layer of prisms (elongation).
The elongated and gyroelongated alternated cubic tilings have the same vertex figure, but are not alike. In the elongated form, each prism meets a tetrahedron at one triangular end and an octahedron at the other. In the gyroelongated form, prisms that meet tetrahedra at both ends alternate with prisms that meet octahedra at both ends.
The gyroelongated triangular prismatic tiling has the same vertex figure as one of the plain prismatic tilings; the two may be derived from the gyrated and plain triangular prismatic tilings, respectively, by inserting layers of cubes.
Referenced
indicessymbol Honeycomb name cell types (# at each vertex) Solids
(Partial)Frames
(Perspective)vertex figure J52
A2'
G2h{4,3,4}:g gyrated alternated cubic tetrahedron (8)
octahedron (6)


triangular orthobicupolaJ61
A?
G3h{4,3,4}:ge gyroelongated alternated cubic triangular prism (6)
tetrahedron (4)
octahedron (3)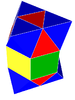

- J62
A?
G4h{4,3,4}:e elongated alternated cubic triangular prism (6)
tetrahedron (4)
octahedron (3)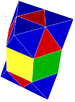


J63
A?
G12{3,6}:g x {∞} gyrated triangular prismatic triangular prism (12) 


J64
A?
G15{3,6}:ge x {∞} gyroelongated triangular prismatic triangular prism (6)
cube (4)


Prismatic stacks
Eleven prismatic tilings are obtained by stacking the eleven uniform plane tilings, shown below, in parallel layers. (One of these honeycombs is the cubic, shown above.) The vertex figure of each is an irregular bipyramid whose faces are isosceles triangles.
The C~2xI~1(∞), [4,4] x [∞], prismatic group
There's only 3 unique honeycombs from the square tiling, but all 6 tiling truncations are listed below for completeness, and tiling images are shown by colors corresponding to each form.
Indices Coxeter-Dynkin
and Schläfli
symbolsHoneycomb name Plane
tilingSolids
(Partial)Tiling J11,15
A1
G22








{4,4} x {∞}Cubic
(Square prismatic)(4.4.4.4) 

J45
A6
G24








t0,1{4,4} x {∞}Truncated/Bitruncated square prismatic (4.8.8) 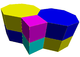

J11,15
A1
G22








t1{4,4} x {∞}Cubic
(Rectified square prismatic)(4.4.4.4) 

J11,15
A1
G22








t0,2{4,4} x {∞}Cubic
(Cantellated square prismatic)(4.4.4.4) 

J45
A6
G24








t0,1,2{4,4} x {∞}Truncated square prismatic
(Omnitruncated square prismatic)(4.8.8) 

J44
A11
G14








s{4,4} x {∞}Snub square prismatic (3.3.4.3.4) 

The G~2xI~1(∞), [6,3] x [∞] prismatic group
Indices Coxeter-Dynkin
and Schläfli
symbolsHoneycomb name Plane
tilingSolids
(Partial)Tiling J42
A5
G26








t0{6,3} x {∞}Hexagonal prismatic (63) 

J46
A7
G19








t0,1{6,3} x {∞}Truncated hexagonal prismatic (3.12.12) 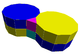

J43
A8
G18








t1{6,3} x {∞}Trihexagonal prismatic (3.6.3.6) 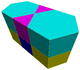

J42
A5
G26








t1,2{6,3} x {∞}Truncated triangular prismatic
Hexagonal prismatic(6.6.6) 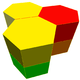

J41
A4
G11








t2{6,3} x {∞}Triangular prismatic (36) 

J47
A9
G16








t0,2{6,3} x {∞}Rhombi-trihexagonal prismatic (3.4.6.4) 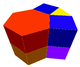

J49
A10
G23








t0,1,2{6,3} x {∞}Omnitruncated trihexagonal prismatic (4.6.12) 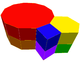

J48
A12
G17








s{6,3} x {∞}Snub trihexagonal prismatic (3.3.3.3.6) 

J65
A11'
G13{3,6}:e x {∞} elongated triangular prismatic (3.3.3.4.4) 

Examples
All 28 of these tessellations are found in crystal arrangements.[citation needed]
The alternated cubic honeycomb is of special importance since its vertices form a cubic close-packing of spheres. The space-filling truss of packed octahedra and tetrahedra was apparently first discovered by Alexander Graham Bell and independently re-discovered by Buckminster Fuller (who called it the octet truss and patented it in the 1940s). [2] [3] [4] [5]. Octet trusses are now among the most common types of truss used in construction.
Noncompact forms
Examples (partially drawn) 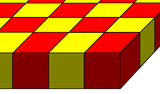
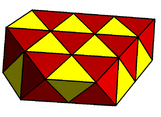
Cubic slab honeycomb







Alternated hexagonal slab honeycomb







If cells are allowed to be uniform tilings, more uniform honeycombs can be defined:
Families:
 xA1: [4,4]x[ ]
xA1: [4,4]x[ ] 





 Cubic prismatic slab honeycomb (3 forms)
Cubic prismatic slab honeycomb (3 forms) xA1: [6,3]x[ ]
xA1: [6,3]x[ ] 





 Tri-hexagonal prismatic slab honeycomb (8 forms)
Tri-hexagonal prismatic slab honeycomb (8 forms) xA1: (3 3 3)x[ ]
xA1: (3 3 3)x[ ] 



 Triangular prismatic slab (No new forms)
Triangular prismatic slab (No new forms) xA1xA1: [∞]x[ ]x[ ]
xA1xA1: [∞]x[ ]x[ ] 





 =
= 





 Cubic column honeycomb (1 form)
Cubic column honeycomb (1 form)- I2(p)x
 : [p]x[∞]
: [p]x[∞] 





 Prismatic column honeycomb
Prismatic column honeycomb  x
x xA1: [∞]x[∞]x[ ] = [4,4]x[ ] -
xA1: [∞]x[∞]x[ ] = [4,4]x[ ] - 







 =
= 





 (Same as cubic slab honeycomb family)
(Same as cubic slab honeycomb family)
Hyperbolic forms
 The {5,3,4} honeycomb in 3D hyperbolic space, viewed in perspective
The {5,3,4} honeycomb in 3D hyperbolic space, viewed in perspective Main article: Convex uniform honeycombs in hyperbolic space
Main article: Convex uniform honeycombs in hyperbolic spaceThere are 9 Coxeter group families of compact uniform honeycombs in hyperbolic 3-space, generated as Wythoff constructions, and represented by ring permutations of the Coxeter-Dynkin diagrams for each family.
From these 9 families, there are a total of 76 unique honeycombs generated:
- [3,5,3] :






 - 9 forms
- 9 forms - [5,3,4] :






 - 15 forms
- 15 forms - [5,3,5] :






 - 9 forms
- 9 forms - [5,31,1] :




 - 11 forms (7 overlap with [5,3,4] family, 4 are unique)
- 11 forms (7 overlap with [5,3,4] family, 4 are unique) - (4 3 3 3) :



 - 9 forms
- 9 forms - (4 3 4 3) :




 - 6 forms
- 6 forms - (5 3 3 3) :



 - 9 forms
- 9 forms - (5 3 4 3) :




 - 9 forms
- 9 forms - (5 3 5 3) :




 - 6 forms
- 6 forms
The full list of hyperbolic uniform honeycombs has not been proven and an unknown number of non-Wythoffian exist. One known example is in the {3,5,3} family.
There are also 23 noncompact Coxeter groups of rank 4. These families can produce uniform honeycombs with unbounded facets or vertex figure, including ideal vertices at infinity:
Hyperbolic noncompact groups 7 



 ,
, 



 ,
, 



 ,
, 



 ,
, 



 ,
, 



 ,
, 




7 





 ,
, 





 ,
, 





 ,
,





 ,
, 





 ,
, 





 ,
, 






6 



 ,
, 



 ,
, 



 ,
, 



 ,
, 



 ,
, 
3 



 ,
, 



 ,
, 




References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)
- George Olshevsky, (2006, Uniform Panoploid Tetracombs, Manuscript (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Branko Grünbaum, (1994) Uniform tilings of 3-space. Geombinatorics 4, 49 - 56.
- Norman Johnson (1991) Uniform Polytopes, Manuscript
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Chapter 5: Polyhedra packing and space filling)
- Critchlow, Keith (1970). Order in Space: A design source book. Viking Press. ISBN 0-500-34033-1.
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [6]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
- A. Andreini, (1905) Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 75–129.
- D. M. Y. Sommerville, (1930) An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, . 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes
External links
- Weisstein, Eric W., "Honeycomb" from MathWorld.
- Uniform Honeycombs in 3-Space VRML models
- Elementary Honeycombs Vertex transitive space filling honeycombs with non-uniform cells.
- Uniform partitions of 3-space, their relatives and embedding, 1999
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- octet truss animation
- Review: A. F. Wells, Three-dimensional nets and polyhedra, H. S. M. Coxeter (Source: Bull. Amer. Math. Soc. Volume 84, Number 3 (1978), 466-470.)
- Richard Klitzing, 3D, Euclidean tesselations
Categories:- Honeycombs (geometry)
Wikimedia Foundation. 2010.

