- Parsec
-
For other uses, see Parsec (disambiguation).
1 parsec = SI units 30.857×1012 km 30.857×1015 m Astronomical units 206.26×103 AU 3.26156 ly US customary / Imperial units 19.174×1012 mi 101.24×1015 ft The parsec (symbol: pc) is a unit of length used in astronomy. It is about 3.26 light-years, or just under 31 trillion (3.1×1013) kilometres (about 19 trillion miles).
The name parsec is "an abbreviated form of 'a distance corresponding to a parallax of one second'."[1] It was coined in 1913 at the suggestion of British astronomer Herbert Hall Turner. A parsec is the distance from the Sun to an astronomical object which has a parallax angle of one arcsecond.
Contents
History and derivation
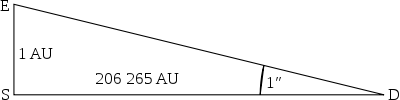
See also: Stellar parallax A parsec is the distance from the Sun to an astronomical object which has a parallax angle of one arcsecond. (1 AU and 1 pc are not to scale (1 pc = 206265 AU))
A parsec is the distance from the Sun to an astronomical object which has a parallax angle of one arcsecond. (1 AU and 1 pc are not to scale (1 pc = 206265 AU))
The parsec is equal to the length of the adjacent side of an imaginary right triangle in space. The two dimensions that this triangle is based on are the angle (which is defined as 1 arcsecond), and the opposite side (which is defined as 1 Astronomical Unit, which is the distance from the Earth to the sun). Using these two measurements, along with the rules of trigonometry, the length of the adjacent side (the parsec) can be found.
One of the oldest methods for astronomers to calculate the distance to a star was to record the difference in angle between two measurements of the position of the star in the sky. The first measurement was taken from the Earth on one side of the Sun, and the second was taken half a year later when the Earth was on the opposite side of the Sun. Thus, the distance between the two measurements was known to be twice the distance between the Earth and the Sun. The distance to the star could be calculated using trigonometry. The first successful direct measurements of an object at interstellar distances were undertaken by German astronomer Friedrich Wilhelm Bessel in 1838, who used this approach to calculate the distance of 61 Cygni.[2]
The parallax of a star is taken to be half of the angular distance that a star appears to move relative to the celestial sphere as Earth orbits the Sun. Equivalently, it is the subtended angle, from that star's perspective, of the semi-major axis of Earth's orbit. The star, the sun and the earth form the corners of an imaginary right triangle in space: the right angle is the corner at the sun, and the corner at the star is the parallax angle. The length of the opposite side to the parallax angle is the distance from the Earth to the Sun (defined as 1 astronomical unit (AU)), and the length of the adjacent side gives the distance from the sun to the star. Therefore, given a measurement of the parallax angle, along with the rules of trigonometry, the distance from the sun to the star can be found. A parsec is defined as the length of the adjacent side of this right triangle in space when the parallax angle is 1 arcsecond.
The use of the parsec as a unit of distance follows naturally from Bessel's method, since distance in parsecs can be computed simply as the reciprocal of the parallax angle in arcseconds (i.e. if the parallax angle is 1 arcsecond, the object is 1 pc distant from the sun; If the parallax angle is 0.5 arcsecond, the object is 2 pc distant; etc.). No trigonometric functions are required in this relationship because the very small angles involved mean that the approximate solution of the skinny triangle can be applied.
Though it may have been used before, the term parsec was first mentioned in an astronomical publication in 1913. Astronomer Royal Frank Watson Dyson expressed his concern for the need of a name for that unit of distance. He proposed the name astron, but mentioned that Carl Charlier had suggested siriometer and Herbert Hall Turner had proposed parsec.[3] It was Turner's proposal that stuck.
Calculating the value of a parsec
In the diagram above (not to scale), S represents the Sun, and E the Earth at one point in its orbit. Thus the distance ES is one astronomical unit (AU). The angle SDE is one arcsecond (1/3600 of a degree) so by definition D is a point in space at a distance of one parsec from the Sun. By trigonometry, the distance SD is
Using small-angle approximation,
One AU ≈ 149597870700 metres, so 1 parsec ≈ 3.085678×1016 m ≈ 3.261564 ly.
A corollary is that 1 parsec is also the distance from which a disc with a diameter of 1 AU must be viewed for it to have an angular diameter of 1 arcsecond (by placing the observer at D and a diameter of the disc on ES).
Usage and measurement
The parallax method is the fundamental calibration step for distance determination in astrophysics; however, the accuracy of ground-based telescope measurements of parallax angle is limited to about 0.01 arcseconds, and thus to stars no more than 100 pc distant.[4] This is because the Earth’s atmosphere limits the sharpness of a star's image.[5] Space-based telescopes are not limited by this effect and can accurately measure distances to objects beyond the limit of ground-based observations. Between 1989 and 1993, the Hipparcos satellite, launched by the European Space Agency (ESA), measured parallaxes for about 100,000 stars with an astrometric precision of about 0.97 milliarcseconds, and obtained accurate measurements for stellar distances of stars up to 1,000 pc away.[6][7] NASA's FAME satellite was to have been launched in 2004, to measure parallaxes for about 40 million stars with sufficient precision to measure stellar distances of up to 2,000 pc. However, the mission's funding was withdrawn by NASA in January 2002.[8] ESA's Gaia satellite, due to be launched in late 2012, is intended to measure one billion stellar distances to within 20 microarcseconds, producing errors of 10% in measurements as far as the Galactic Center, about 8,000 pc away in the constellation of Sagittarius.[9]
Distances in parsecs
Distances less than a parsec
Distances measured in fractions of a parsec usually involve objects within a single star system. So, for example:
- One astronomical unit (AU), the distance from the Sun to the Earth, is 4.85×10−6 pc.
- The most distant space probe, Voyager 1, was 5.64×10−4 pc away from Earth as of May 2011[update]. It took Voyager 30 years to cover that distance.
- The Oort cloud is estimated to be approximately 0.6 pc in diameter.
Parsecs and kiloparsecs
 The jet erupting from this active galactic nucleus is thought to be 1.5 kiloparsecs long. (image from Hubble Space Telescope)
The jet erupting from this active galactic nucleus is thought to be 1.5 kiloparsecs long. (image from Hubble Space Telescope)
Distances measured in parsecs include distances between nearby stars, such as those in the same spiral arm or globular cluster. A distance of one thousand parsecs (approximately 3,262 ly) is commonly denoted by the kiloparsec (kpc). Astronomers typically use kiloparsecs to measure distances between parts of a galaxy, or within groups of galaxies. So, for example:
- One parsec is approximately 3.262 light-years.
- The nearest known star to the Earth, other than the Sun, Proxima Centauri, is 1.29 parsecs away.
- The center of the Milky Way is about 8 kpc from the Earth, and the Milky Way is about 30 kpc across.
- The Andromeda Galaxy (M31) is slightly less than 800 kpc away from the Earth.
Megaparsecs and gigaparsecs
A distance of one million parsecs (approximately 3,262,000 light-years) is commonly denoted by the megaparsec (Mpc). Astronomers typically measure the distances between neighbouring galaxies and galaxy clusters in megaparsecs.
Galactic distances are sometimes given in units of Mpc/h (as in "50/h Mpc"). h is a parameter in the range [0.5,0.75] reflecting the uncertainty in the value of the Hubble constant H for the rate of expansion of the universe: h = H / (100 km/s/Mpc). The Hubble constant becomes relevant when converting an observed redshift z into a distance d using the formula d ≈ (c / H) × z.[10]
One gigaparsec (Gpc) is one billion parsecs—one of the largest distance measures commonly used. One gigaparsec is about 3.262 billion light-years, or roughly one fourteenth of the distance to the horizon of the observable universe (dictated by the cosmic background radiation). Astronomers typically use gigaparsecs to measure large-scale structures such as the size of, and distance to, the CfA2 Great Wall; the distances between galaxy clusters; and the distance to quasars.
For example:
- The Andromeda Galaxy is 0.77 Mpc away from the Earth.
- The nearest large galaxy cluster, the Virgo Cluster, is about 16.5 Mpc[11] away from the Earth.
- The galaxy RXJ1242-11, observed to have a supermassive black hole core similar to the Milky Way's, is about 200 Mpc away from the Earth.
- The particle horizon (the boundary of the observable universe) has a radius of about 14 Gpc (46.5 billion light-years).[12]
Volume units
To determine the number of stars in the Milky Way Galaxy, volumes in cubic kiloparsecs[13] (kpc3) are selected in various directions. All the stars in these volumes are counted and the total number of stars statistically determined. The number of globular clusters, dust clouds and interstellar gas is determined in a similar fashion. To determine the number of galaxies in superclusters, volumes in cubic megaparsecs[13] (Mpc3) are selected. All the galaxies in these volumes are classified and tallied. The total number of galaxies can then be determined statistically. The huge void in Bootes[14] is measured in cubic megaparsecs. In cosmology, volumes of cubic gigaparsecs[13] (Gpc3) are selected to determine the distribution of matter in the visible universe and to determine the number of galaxies and quasars. The Sun is alone in its cubic parsec,[13] (pc3) but in globular clusters the stellar density per cubic parsec could be from 100 to 1,000.
See also
- Conversion of units
- Cosmic distance ladder
- Light-year
- Small-angle approximation
- Spectroscopic parallax
References and notes
- ^ Dyson, F. W., Stars, Distribution and drift of,The distribution in space of the stars in Carrington's Circumpolar Catalogue. In: Monthly Notices of the Royal Astronomical Society, Vol. 73, p.334-342. March, 1913.[1]
"There is a need for a name for this unit of distance. Mr. Charlier has suggested Siriometer ... Professor Turner suggests PARSEC, which may be taken as an abbreviated form of 'a distance corresponding to a parallax of one second'." - ^ Bessel, FW, "Bestimmung der Entfernung des 61sten Sterns des Schwans" (1838) Astronomische Nachrichten, vol. 16, pp. 65–96.
- ^ Dyson, F. W., "The distribution in space of the stars in Carrington's Circumpolar Catalogue" (1913) Monthly Notices of the Royal Astronomical Society, vol. 73, pp. 334–42, p. 342 fn..
- ^ Richard Pogge, Astronomy 162, Ohio State.
- ^ jrank.org, Parallax Measurements
- ^ "The Hipparcos Space Astrometry Mission". http://www.rssd.esa.int/index.php?project=HIPPARCOS. Retrieved August 28, 2007.
- ^ Catherine Turon, From Hipparchus to Hipparcos
- ^ FAME news, 25 January 2002.
- ^ GAIA from ESA.
- ^ "Galaxy structures: the large scale structure of the nearby universe". http://pil.phys.uniroma1.it/twiki/bin/view/Pil/GalaxyStructures. Retrieved May 22, 2007.
- ^ Mei, S. et al 2007, ApJ, 655, 144
- ^ "Misconceptions about the Big Bang". http://www.scientificamerican.com/article.cfm?id=misconceptions-about-the-2005-03&page=5. Retrieved January 8, 2010.
- ^ a b c d
1 pc3 ≈ 2.938×1049 m3 1 kpc3 ≈ 2.938×1058 m3 1 Mpc3 ≈ 2.938×1067 m3 1 Gpc3 ≈ 2.938×1076 m3 - ^ Astrophysical Journal, Harvard
External links
- Guidry, Michael. "Astronomical Distance Scales". Astronomy 162: Stars, Galaxies, and Cosmology. University of Tennessee, Knoxville. http://csep10.phys.utk.edu/guidry/violence/distances.html. Retrieved 2010-03-26.
Units of length used in Astronomy Astronomical system of units Earth radius ( or RE) · Light-second (ls) · Solar radius (
or RE) · Light-second (ls) · Solar radius ( ) · gigametre (Gm) · Astronomical unit (AU) · light-year (ly) · parsec (pc) · kiloparsec (kpc) · megaparsec (Mpc) · gigaparsec (Gpc)
) · gigametre (Gm) · Astronomical unit (AU) · light-year (ly) · parsec (pc) · kiloparsec (kpc) · megaparsec (Mpc) · gigaparsec (Gpc)See Also: Cosmic distance ladder · Orders of magnitude (length) · Conversion of units Categories:- Units of length
- Units of measure in astronomy
- Parallax
Wikimedia Foundation. 2010.